Нетрадиционные способы умножения многозначных чисел
Исследовательская работа по математике в начальной школе
Краткая аннотация исследовательской работыКаждый школьник умеет умножать многозначные числа «столбиком». В данной работе автор обращает внимание на существование альтернативных способов умножения, доступных младшим школьникам, которые могут «нудные» вычисления превратить в весёлую игру.
В работе рассматриваются шесть нетрадиционных способов умножения многозначных чисел, используемые в различные исторические эпохи: русский крестьянский, решетчатый, маленький замок, китайский, японский, по таблице В.Оконешникова.
Проект предназначен для развития познавательного интереса к изучаемому предмету, для углубления знаний в области математики.
Оглавление
Введение 3
Глава 1. Альтернативные способы умножения 4
1.1. Немного истории 4
1.2. Русский крестьянский способ умножения 4
1.3. Умножение способом «Маленький замок» 5
1.4. Умножение чисел методом «ревность» или «решётчатое умножение» 5
1.5. Китайский способ умножения 5
1.6. Японский способ умножения 6
1.7. Таблица Оконешникова 6
1.8.Умножение столбиком. 7
Глава 2. Практическая часть 7
2.1. Крестьянский способ 7
2.2. Маленький замок 7
2.3. Умножение чисел методом «ревность» или «решётчатое умножение» 7
2.4. Китайский способ 8
2.5. Японский способ 8
2.6. Таблица Оконешникова 8
2.7. Анкетирование 8
Заключение 9
Приложение 10
«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».
Б. Паскаль
Введение
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе. Возник вопрос: а есть ли еще какие-нибудь альтернативные способы вычислений? Мне захотелось изучить их более подробно. В поисках ответа на возникшие вопросы было проведено данное исследование.
Цель исследования: выявление нетрадиционных способов умножения для изучения возможности их применения.
В соответствии с поставленной целью нами были сформулированные следующие задачи:
- Найти как можно больше необычных способов умножения.
- Научиться их применять.
- Выбрать для себя самые интересные или более легкие, чем те, которые предлагаются в школе, и использовать их при счете.
- Проверить на практике умножения многозначных чисел.
- Провести анкетирование учащихся 4-х классов
Объект исследования: различные нестандартные алгоритмы умножения многозначных чисел
Предмет исследования: математическое действие «умножение»
Гипотеза: если существуют стандартные способы умножения многозначных чисел, возможно, есть и альтернативные способы.
Актуальность: распространение знаний об альтернативных способах умножения.
Практическая значимость. В ходе работы было решено множество примеров и создан альбом, в который включены примеры с различными алгоритмами умножениями многозначных чисел несколькими альтернативными способами. Это может заинтересовать одноклассников для расширения математического кругозора и послужит началом новых экспериментов.
Глава 1. Альтернативные способы умножения
1.1. Немного историиТе способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы современный школьник мог отправиться на пятьсот лет назад, он поразил бы всех быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Особенно трудны в старину были действия умножения и деления.
В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще способы, скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках». И все эти приемы умножения соперничали друг с другом и усваивались с большим трудом.
Рассмотрим наиболее интересные и простые способы умножения.
1.2. Русский крестьянский способ умножения
В России 2-3 века назад среди крестьян некоторых губерний был распространен способ, который не требовал знание всей таблицы умножения. Надо было лишь уметь умножать и делить на 2. Этот способ получил название крестьянского.
Чтобы перемножить два числа, их записывали рядом, а затем левое число делили на 2, а правое умножали на 2. Результаты записывать в столбик, пока слева не останется 1. Остаток отбрасывается. Вычёркиваем те строки, в которых слева стоят чётные числа. Оставшиеся числа в правом столбце - складываем.
1.3. Умножение способом «Маленький замок»
Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности» (1494г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок».
Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.
Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.
1.4. Умножение чисел методом «ревность» или «решётчатое умножение»
Второй способ Лука Пачоли носит название «ревность» или «решётчатое умножение».
Сначала рисуется прямоугольник, разделённый на квадраты. Затем квадратные клетки делятся по диагонали и «…получается картинка, похожая на решётчатые ставни-жалюзи, - пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».
Перемножая каждую цифру первого множителя с каждой цифрой второго, записываются произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры произведения получают сложением цифр в косых полосах. Результаты сложений записываются под таблицей, а также справа от неё.
1.5. Китайский способ умножения
Теперь представим метод умножения, бурно обсуждаемый в Интернете, который называют китайским. При умножении чисел считаются точки пересечения прямых, которые соответствуют количеству цифр каждого разряда обоих множителей.
1.6. Японский способ умножения
Японский способ умножения – это графический способ с использованием кругов и линий. Не менее забавный и интересный чем китайский. Даже чем-то на него похож.
1.7. Таблица Оконешникова
Кандидат философских наук Василий Оконешников, по совместительству изобретатель новой системы устного счёта, считает, что школьники смогут научиться устно складывать и умножать миллионы, биллионы и даже секстиллионы с квадриллионами. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.
По мысли учёного, прежде чем стать вычислительным «компьютером», необходимо вызубрить созданную им таблицу.
Таблица разделена на 9 частей. Расположены они по принципу мини калькулятора: слева в нижнем углу «1», справа в верхнем углу «9». Каждая часть – таблица умножения чисел от 1 до 9 (по той же «кнопочной» система). Для того, чтобы умножить любое число, например, на 8, мы находим большой квадрат, соответствующий числу 8 и выписываем из этого квадрата числа, соответствующие цифрам многозначного множителя. Полученные числа складываем особо: первая цифра остаётся без изменения, а все остальные попарно складываются. Получившееся число и будет результатом умножения.
Если при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.
Новая методика была опробована в нескольких российских школах и университетах. Минобразования РФ разрешило публиковать в тетрадях в клеточку вместе с привычной таблицей Пифагора новую таблицу умножения – пока просто для знакомства.
1.8. Умножение столбиком.
Не многие знают, что автором нашего привычного способа умножения столбиком многозначного числа на многозначное следует считать Адама Ризе (Приложение 7). Этот алгоритм считается самым удобным.
Глава 2. Практическая часть
Осваивая перечисленные способы умножения, было решено множество примеров, оформлен альбом с образцами различных алгоритмов вычислений. (Приложение). Рассмотрим алгоритм вычислений на примерах.
2.1. Крестьянский способ
Умножим 47 на 35 (Приложение 1),
-запишем числа на одной строчке, проведём между ними вертикальную черту;
-левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
-деление заканчивается, когда слева появится единица;
-вычёркиваем те строчки, в которых стоят слева чётные числа;
-оставшиеся справа числа складываем – это результат.
35 + 70 + 140 + 280 + 1120 = 1645.
Вывод. Способ удобен тем, что достаточно знать таблицу только на 2. Однако при работе с большими числами он очень громоздкий. Удобен для работы с двузначными числами.
2.2. Маленький замок
(Приложение 2). Вывод. Способ очень похож на наш современный «столбик». Да еще и сразу определяются цифры старших разрядов. Это бывает важно, если нужно быстро оценить величину.
2.3. Умножение чисел методом «ревность» или «решётчатое умножение»
Умножим, например, числа 6827 и 345 (Приложение 3):
1. Вычерчиваем квадратную сетку и пишем один из множителей над колонками, а второй - по высоте.
2. Умножаем число каждого ряда последовательно на числа каждой колонки. Последовательно умножаем 3 на 6, на 8, на 2 и на 7 и т.д.
4. Складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали.
Из результатов сложения цифр по диагоналям составляется число 2355315, которое и является произведением чисел 6827 и 345, то есть 6827 ∙ 345 = 2355315.
Вывод. Способ «решетчатое умножение» ничуть не хуже, чем общепринятый. Он даже проще, поскольку в клетки таблицы заносятся числа прямо из таблицы умножения без одновременного сложения, присутствующего в стандартном методе.
2.4. Китайский способ
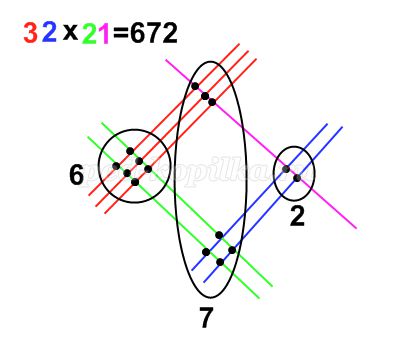
Предположим надо умножить 12 на 321(Приложение 4). На листе бумаги поочередно рисуем линии, количество которых определяется из данного примера.
Рисуем первое число – 12. Для этого сверху вниз, слева на право, рисуем:
одну зелёную палочку (1)
и две оранжевых (2).
Рисуем второе число – 321, снизу вверх, слева на право:
три голубых палочки (3);
две красные (2);
одну сиреневую (1).
Теперь простым карандашом отделяем точки пересечения и приступим к их подсчёту. Двигаемся справа налево (по часовой стрелке): 2, 5, 8, 3.
Полученный результат прочитаем слева направо – 3852
Вывод. Интересный способ, но проводить 9 прямых при умножении на 9 как-то долго и неинтересно, а потом еще точки пересечения считать. Без сноровки сложно разобраться в делении числа на разряды. В общем, без таблицы умножения не обойтись!
2.5. Японский способ
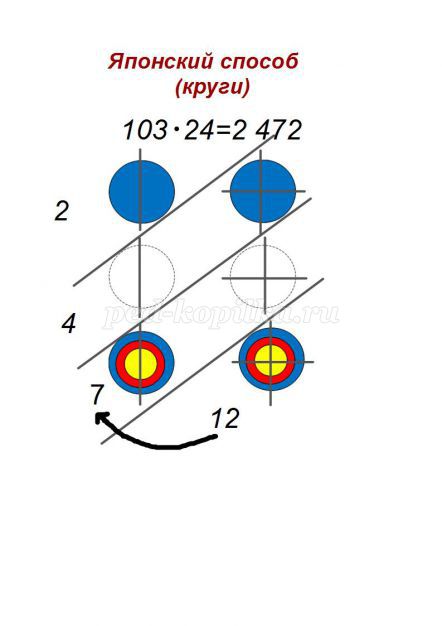
Умножим 12 на 34 (Приложение 5). Так как второй множитель двузначное число, а первая цифра первого множителя 1, строим два одиночных круга в верхней строке и два двоичных круга в нижней строке, так как вторая цифра первого множителя равна 2.
Так как первая цифра второго множителя 3, а вторая 4, делим круги первого столбца на три части, второго столбца на четыре части.
Количество частей, на которые разделились круги и является ответом, то есть 12 х 34 = 408.
Вывод. Способ очень похож на китайский графический. Только прямые заменены кругами. Легче определять разряды у числа, однако рисовать круги – менее удобно.
2.6. Таблица Оконешникова
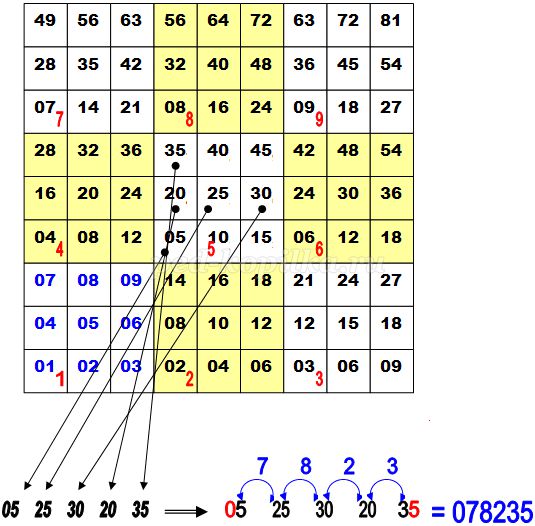
Требуется умножить 15647 х 5. Сразу вспоминаем большую «кнопку» 5 (она посередине) и на ней мысленно находим маленькие кнопочки 1, 5, 6, 4, 7 (они также расположены, как на калькуляторе). Им соответствуют числа 05, 25, 30, 20, 35. Полученные числа складываем: первая цифра 0 (остаётся без изменения), 5 мысленно складываем с 2, получаем 7 – это вторая цифра результата, 5 складываем с 3, получаем третью цифру - 8, 0+2=2, 0+3=3 и остаётся последняя цифра произведения – 5. В результате получилось 78 235.
Вывод. Способ очень удобный, но нужно выучить наизусть или всегда иметь под рукой таблицу.
2.7. Анкетирование учащихся
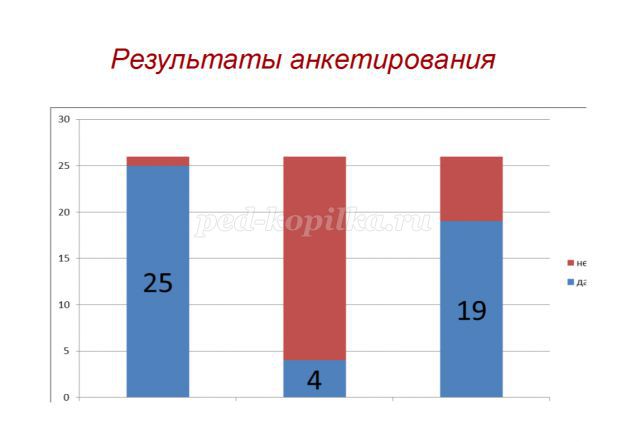
Было проведено анкетирование четвероклассников. Приняли участие 26 человек (Приложение 8). На основании анкетирования выявлено, что все опрошенные умеют умножать традиционным способом. А вот о нетрадиционных способах умножения большинство ребят не знают. И есть желающие познакомиться с ними.
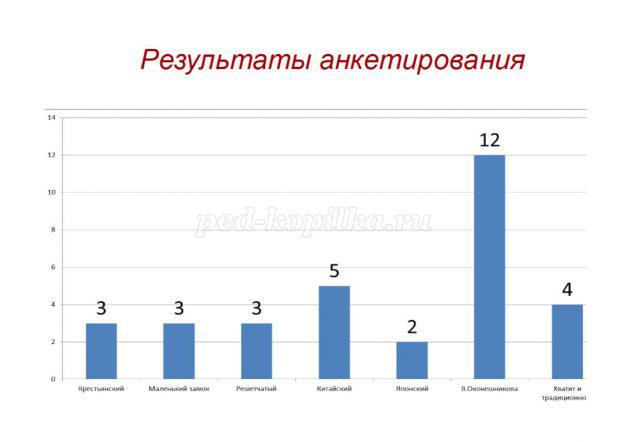
После первичного анкетирования было проведено внеклассное занятие «Умножение с увлечением», на котором ребята познакомились с альтернативными алгоритмами умножения. После чего был проведен опрос с целью выявить наиболее понравившиеся способы. Безусловным лидером стал самый современный метод Василия Оконешникова. (Приложение 9)
Заключение
Научившись считать всеми представленными способами, я считаю, что наиболее удобный метод умножения является способ «Маленький замок» - ведь он так похож на наш нынешний!
Из всех найденных мною необычных способов счета более интересным показался способ «Японский». Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне. Я его использую при умножении не слишком больших чисел. Очень удобно его использовать при умножении двузначных чисел.
Таким образом, я достигла цели моего исследования – изучила и научилась применять нетрадиционные способы умножения многозначных чисел. Моя гипотеза подтвердилась – я овладела шестью альтернативными способами и выяснила, что это еще не все возможные алгоритмы.
Изученные мною нетрадиционные методы умножения очень интересны и имеют право на существование. А в некоторых случаях ими даже проще пользоваться. Считаю, что о существовании этих методов можно рассказывать в школе, дома и удивить своих друзей и знакомых.
Пока мы только изучали и анализировали уже известные способы умножения. Но кто знает, возможно, в будущем мы сами сможем открыть новые способы умножения. Также я не хочу останавливаться на достигнутом и продолжить изучение нетрадиционных способов умножения.
Список источников информации
1. Список литературы
1.1. Арутюнян Е., Левитас Г. Занимательная математика. - М.: АСТ - ПРЕСС, 1999. - 368 с.
1.2. Беллюстина В. Как постепенно дошли люди до настоящей арифметики. - ЛКИ ,2012.-208 с.
1.3. Депман И. Рассказы о математике. – Ленинград.: Просвещение, 1954. – 140 с.
1.4. Ликум А. Все обо всем. Т. 2. - М.: Филологическое общество «Слово», 1993. - 512 с.
1.5. Олехник С. Н., Нестеренко Ю. В., Потапов М. К.. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.
1.6. Перельман Я.И. Занимательная арифметика. - М.: Русанова, 1994 – 205с.
1.7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л.: Лениздат, 1941 — 12 с.
1.8. Савин А.П. Математические миниатюры. Занимательная математика для детей. - М.: Детская литература, 1998 - 175 с.
1.9. Энциклопедия для детей. Математика. – М.: Аванта +, 2003. – 688 с.
1.10. Я познаю мир: Детская энциклопедия: Математика/ сост. Савин А.П., Станцо В.В., Котова А.Ю. - М.: ООО «Издательство АСТ», 2000. - 480 с.
2. Другие источники информации
Интернет – ресурсы:
2.1. Корнеев А.А. Феномен русского умножения. История. [Электронный ресурс]
Приложения
Приложение 1. Крестьянский способ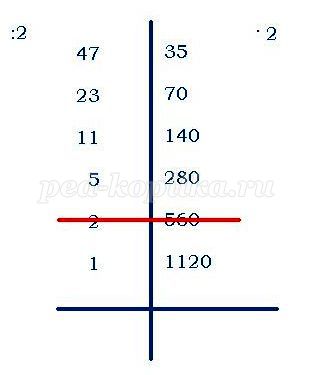
Приложение 2. Маленький замок

Приложение 3. Решетчатый

Приложение 4. Китайский способ (графический)
Приложение 5.Японский способ (круги)
Приложение 6. Таблица Василия Оконешникова
Приложение 7. Умножение столбиком
Адам Ризе (27 марта 1492 —30 марта 1559) — германский математик, выдающийся учитель счёта.

Приложение 8. Результаты первичного анкетирования
Приложение 9. Наиболее понравившиеся способы умножения (по результатам опроса одноклассников)
Рекомендуем посмотреть:
 Конспект урока математики в 1 классе
Конспект урока математики в 1 классе
 Математическое домино для 3-4 класса
Математическое домино для 3-4 класса
 Исследовательская работа по математике с презентацией, 5 класс
Исследовательская работа по математике с презентацией, 5 класс
 Задачи по математике для учащихся 1-4 класса. Государственная Третьяковская галерея
Задачи по математике для учащихся 1-4 класса. Государственная Третьяковская галерея
Похожие статьи:
Олимпиадные задания с ответами по математике для 1-4 классов
Математические кроссворды и головоломки с ответами для 1-4 класса
Участник №174 профессионального конкурса для педагогов на лучшую методическую разработку с 20 февраля по 20 мая 2016 года
|
|
Автор: Анна Валерьевна Демешко
Опубликовано: 2928 дней назад (14 апреля 2016)
Просмотров: 38770
Блог: Демешко Анны Валерьевны
Рубрика: Научно-практическая конференция
|
0 Голосов: 0 |
| # 14 апреля 2016 в 17:54 0 |
| # 14 апреля 2016 в 18:08 0 | ||
|
| # 15 апреля 2016 в 12:58 0 | ||
|
| # 8 мая 2018 в 21:58 0 |
| Анна Валерьевна, таблица умножения не Земного происхождения и возможно Пифагор не первый кто понял это. Есть ли желание открыть новые тайны в умножении? |



