Моделирование решения целочисленных задач

Биглова И.И. учитель информатики СОШ №146 г. Казань
Описание работы
Настоящая работа представляет собой методическую разработку, которая предназначена учителю информатики при прохождении темы "Информационные модели".
Решение многих целочисленных задач связано с подбором значений переменных. Подбор значений можно осуществлять вручную на бумаге или в уме. При этом достаточно легко ошибиться: или неверно подсчитать значения вычисляемых переменных, или просто потерять какие-то наборы переменных. Чтобы избежать многих ошибок, можно воспользоваться электронными таблицами. Использование электронных таблиц также позволить сделать процесс решения таких задач гораздо проще и нагляднее и получить электронные модели различных этапов процесса решения.

Процесс моделирования рассмотрим для двух задач из книги Е.В. Галкина «Нестандартные задачи по математике» издательства «Просвещение» - «Учебная литература», М, 1996 г.
Задача 1. Ученику дали задание, состоящее из 12 задач. За каждую правильно решенную задачу он получает 5 баллов, за неверно решенную с него снимают 3 балла; если же он задачу не решал, то получает за нее 0 баллов. В результате он набрал 11 баллов. Сколько задач ученик решил правильно?
Задачу можно описать системой уравнений. Первое уравнение 5*x-3*y+0*z = 11, или 5*x-3*y = 11, а второе уравнение x+y+z = 12. В уравнениях величина x означает количество правильно решенных задач, величина y означает количество неправильно решенных задач, а величина z - количество нерешенных задач. Значениями переменных должны быть целые неотрицательные числа. Из второго уравнения следует, что значения всех трех переменных ограничены числом 12. Для перебора значений переменных x и y воспользуемся электронными таблицами. В столбце с именем A будем получать значения x, в столбце с именем B – значения y, в столбце с именем C – значения выражения 5*x-3*y. Вначале зададим x=0. Для этого варианта электронные таблицы не понадобятся, поскольку уравнение 5*x-3*y = 11 преобразуется в достаточно простое уравнение -3*y = 11. Решая его, получим y=-11/3. Нецелое значение не может быть решением задачи. Теперь перейдем к использованию электронных таблиц. Для этого зададим x=1, а значения y будем перебирать. При этом в столбце C будут вычисляться значения выражения 5*x-3*y . Как только в этом столбце появится число 11, значит решение будет найдено. Поскольку x + y<=12, то самым большим значением для y может быть число 11, то есть y=0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11. Данный этап решения задачи отображен на рисунке 1.

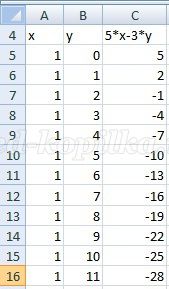
Рисунок 1.

В столбце C нужного нам числа 11 нет. Следовательно, надо перейти к новому этапу решения задачи, то есть к x=2. Значениями величины y в этом случае могут быть числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Этот этап решения задачи отображен на рисунке 2.

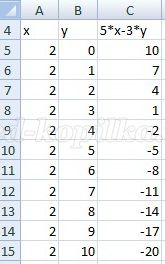
Рисунок 2.
Вновь в столбце C нужного нам числа 11 нет. При x= 3 также не получим число 11 в столбце C. Однако, при x=4 такое число будет получено.

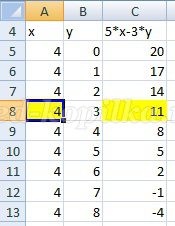
Рисунок 3.
Ответ на решенную задачу находится в столбце A, а это число 4.
Теперь рассмотрим вторую задачу.
Задача2. Решите в целых числах x, y и z систему уравнений
x + y + z= 6,
x + yz = 7.
Данная задача сложнее первой, так как значениями переменных могут быть как положительные, так и отрицательные числа. Для ее решения вычтем из второго уравнения первое. Получим yz-(y+z)=1. Решим вначале задачу математически.
Случай 1. Решим это уравнение относительно y. Раскроем скобки yz-y-z=1, преобразуем y(z-1)=z+1, получим y = (z+1)/(z-1). При y = 0 z = -1, следовательно, x = 7. Одно решение найдено.
Случай 2. Теперь решим уравнение yz-y-z = 1 относительно z. z(y-1) = y+1, z = (y+1) /(y-1). При y = -1, z = 0, x=7. Теперь найдено второе решение.
Как найти другие решения?
Случай 3. y > 0, z < 0. Рассмотрим выражение yz-(y+z). Пусть z = -k, k > 0. Тогда –ky-(y-k) = -ky-y+k. Приравняем к 1 выражение -ky-y+k. Получим -ky-y+k = 1, -y(k+1) = 1-k, y = -(k-1)/(k+1). Выражение для y будет дробным для всех k, кроме k=1, то есть y=0. При y=0 имеем случай1. Новых решений нет.
Случай 4. y < 0, z≠0. Пусть y = -k, k > 0. В выражение yz-(y+z)=1 подставим y = -k, получим –kz-(-k+z) = 1, -kz+k-z = 1, -z(k+1) = 1-k, z = (k-1)/(k+1). Выражение для z будет дробным для всех k, кроме k = 1. При k = 1 z = 0, x = 7, y = -1. Это случай 2. Новых решений нет.
Случай 5. y > 0, z > 0. Пусть уравнение решается относительно y. Тогда y = (z+1)/(z-1). Целое значение этого выражения возможно, когда знаменатель равен 1, то есть при z = 2. Значит при y = 3, x = 1 получим третье решение. Если уравнение решается относительно z, то z = (y+1) /(y-1). При y = 2 значение z будет целым. Поэтому y = 2, z = 3, x = 1 - четвертое решение. Других решений нет.
Перейдем теперь к электронным таблицам и решим задачу еще раз. В столбцы A, E, I, M, Q будем вводить значения для переменной x, в столбцы B, F, J, N, R будем вводить значения для переменной y, а в столбцы C, G, K, O, S формулу для нахождения значения выражения yz-(y+z). Первоначально в столбцы A, E, I, M, Q введем значения 0, 1, -1, 2, -2. Затем в столбцы B, F, J, N, R выберем значения -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6. Таким образом на одном листе рабочей книги получим 5 таблиц для пяти выбранных значений y - для пяти этапов решения задачи (рис. 4).

Рисунок 4.
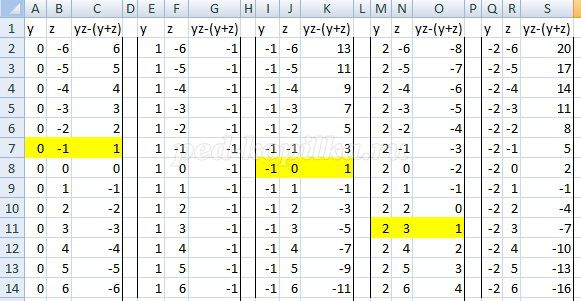
Три решения найдены. Однако необходимо продолжить перебор значений переменных. Дополнительно построим новые 4 таблицы для четырех значений переменной y 3, -3, 4, -4 (рис. 5).

Рисунок 5.
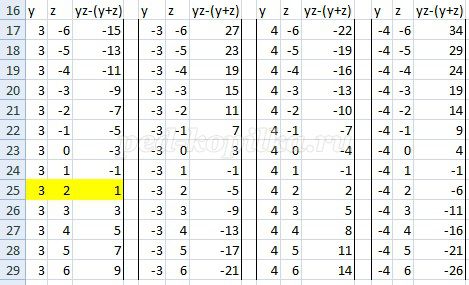
Найдено четвертое решение. Если бы задача не была решена математически, то возник бы вопрос, до каких пор нужно задавать x и y. Для ответа на вопрос придется устанавливать закономерности изменения значений выражения yz-(y+z). Таблиц, имеющихся в двух рисунках достаточно, чтобы эти закономерности установить. Например, выберем z = 1. Во всех девяти таблицах значение выражения yz-(y+z) = -1. Теперь выберем z = -2 и просмотрим значения yz-(y+z) для y = 1, 2, 3, 4. Они отрицательны и убывают. Аналогично и для всех остальных отрицательных значений z. Теперь выберем z = 4 и просмотрим значения yz-(y+z) для y = 1, 2, 3, 4. Они возрастают от -1 до 8. Аналогично и для всех остальных положительных значений z. Они возрастают, за исключением z = 1. Следовательно, дополнительных единичных значений выражения yz-(y+z), кроме тех, которые уже присутствуют в таблицах, при y > 5 получить нельзя. Теперь выберем z = -2 и просмотрим значения yz-(y+z) для y = 0, -1, -2, -3, -4. Они возрастают от 2 до 14. Аналогично и для всех остальных отрицательных значений z. Они возрастают. Теперь выберем z = 4 и просмотрим значения yz-(y+z) для y = 0, -1, -2, -3, -4. Они убывают от -4 до -16. Аналогично и для всех остальных положительных значений z. Они возрастают, за исключением z = 1. Следовательно, дополнительных единичных значений выражения yz-(y+z) при y < -5 получить нельзя. Таким образом, решений четыре. Это x = 7, y = 0, z = -1 ; x = 7, y = -1, z = 0; x = 1, y = 2, z = 3; x = 1, y =3 , z = 2.

Моделирование решения целочисленных задач

Рекомендуем посмотреть:

Похожие статьи: