Решение нестандартных задач в начальной школе. "Задачи на уравнивание"
Решение олимпиадных задач в начальной школе
Задачи на смекалку для младших школьников
Задачи на уравнивание
При решении задач этого вида вспоминается мифологический древнегреческий разбойник по имени Прокруст, отрубавшего или вытягивавшего ноги своим жертвам по длине ложа, на котором он их укладывал. Убрать лишнее или добавить недостающее – суть этого метода.В качестве подготовки к решению задачи этим методом можно рассматривать упражнения, встречающиеся с I класса:
- На полке 8 мишек и зайчиков. Кого больше? На сколько? Как сделать так, чтобы мишек и зайчиков стало поровну?
- На первой полке 7 книг, на второй-5 книг. Что нужно сделать, чтобы книг стало поровну?
Дети должны понять, что уравнять два множества можно, если убрать элементы большего множества или добавить элементы в меньшее множество.
В III классе встречается задача:
В 2-х классах 56 человек, причем в первом классе на 2 человека больше, чем во втором. Сколько человек в каждом классе?
После того, как условие задачи понятно детьми, полезно поставить вопросы:
- Можно ли для решения задачи разделить 56 на 2? Почему?
(Длить на 2 нельзя, так как количество детей в классах разное.)
- Как сделать так, чтобы детей в классах стало поровну?
(Убрать 2 человека из 1 класса или добавить во второй класс.)
- Давайте добавим во второй класс 2 человек, теперь учеников в классах стало поровну.
- Что теперь можем узнать?
(Сколько учеников в первом классе.)
- Как узнать, сколько учеников в первом классе и сколько во 2?
Задача имеет 2 способа решения:
I (56+2): 2=28(чел) – в 1 классе
29-2=27(чел) – во 2 классе
II (56-2): 2=27(чел) – во 2 классе
27+2=39(чел) – в 1 классе
Решая задачи такого типа, дети усваивают, что при вычитании из суммы двух чисел их разности получается удвоенное меньшее число, а при сложении суммы двух чисел и разности число – удвоенное большее число.
Важно, чтобы ученики усвоили сам прием – убрать лишнее или добавить недостающее и пользовались им при решении задач. Ниже привожу задачи, для которых этот прием очень полезен.
1. Сумма 2 чисел равна 1106. Одно из них больше другого на 22. Найди эти числа.
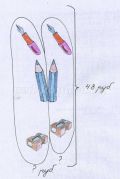
2. 2 карандаша и ластик стоят столько же, сколько 1 карандаш и 4 ластика. Во сколько раз карандаш дороже ластика?
3. У Маши, Саши и Даши вместе 11 воздушных шариков. У Маши на 2 шарика меньше, чем у Даши, а у Саши на 1 шарик больше, чем у Даши. Сколько шариков у Даши?
4. Сумма 5 последовательных чисел равна 875. Найдите эти числа.
5. Трое рыбаков поймали 75 окуней. Один дал для ухи 8 окуней, другой 12, третий 7 и у них осталось поровну. Сколько окуней поймал первый рыбак?
6. У трёх братьев 9 тетрадей, причём у старшего на 1 больше, а у младшего на 1 меньше, чем у среднего. Сколько тетрадей у каждого?
7. В семье 3 братьев. Каждый следующий младше предыдущего на 3 года. А сумма их возрастов равна 15 годам. Сколько лет каждому?
8. Шла по улице семья крокодилов: дед, два отца, два сына. Всем 90 лет. Сколько лет каждому, если каждый отец старше своего сына на 25 лет.
9. В семье 3 братьев. Каждый следующий младше предыдущего на 3 года. А сумма их возрастов равна 15 годам. Сколько лет каждому?
10. Сын лесничего помогал отцу вести подсчет зверей в лесу. После подсчета он сказал отцу: « Я считал медведей, зайцев и волков. Всего зверей 1000, волков на 250 больше, чем медведей, зайцев на 300 больше, чем волков». Услышав такой ответ, лесничий сказал, что такого быть не может. Прав ли лесничий?
11. В газете было написано, что в школе обучается 3688 учащихся, причем мальчиков на 373 больше, чем девочек. Вася Иванов сразу сказал, что в газете допущена ошибка. Как он догадался?
12. Сумма двух натуральных чисел 213. Одно из них меньше другого на 38. Найди числа.
13. Сумма трех последовательных натуральных чисел равна 75. Найдите их.
14. Сумма двух последовательных чисел равна 151. Найдите эти числа.
15. Сумма двух последовательных четных чисел равна 150. Найдите их.
16. Найдите два натуральных числа, если их сумма равна 179, а разность – 61.
Этот метод широко применяется при решении задач, связанных с взвешиванием. Прежде, чем предложить для решения задачу, нужно убедиться в том, что ребята понимают такую аксиому: если весы находятся в равновесии, то с левой и правой чаши можно убрать или положить одинаковые по весу предметы и равновесие не нарушается.
Достичь этого можно, выполнив упражнения:
- На одной чаше весов 2 пакета с мукой, а на другой один такой же пакет и гиря в 1 кг. Сколько весит пакет, если весы находятся в равновесии?
- На левой чаше весов коробка и гиря в 3 кг, а на другой 2 такие же коробки и гиря в 1 кг. Сколько весит одна коробка?
- На левой чаше весов утка и гиря в 1 кг, на правой – гусь. Кто из них тяжелее и на сколько, если весы находятся в равновесии?
- На одной чаше весов 5 яблок, на другой 4 груши. Что тяжелее: яблоко или груша, если весы находятся в равновесии?
- Одна груша весит столько же, сколько 4 сливы. Сколькими сливами можно уравновесить 2 груши?
- Курица и 3 цыпленка весят столько, сколько 1 петух. На одной чаше весов одна курица и 4 цыплёнка, на другой петух. Сколько надо посадить к петуху цыплят, чтобы весы были в равновесии?
- Как с помощью гирь 8 кг, 5 кг и 3 кг отвесить 6 кг крупы одним взвешиванием?
Учитель без труда может составить множество подобных заданий, иллюстрируя их рисунками, моделью весов и гирь или игрушечными весами. После этого можно переходить к сложным задачам.
1. На одной чаше весов 6 одинаковых пачек чая и гиря 50 г, на другой такая же пачка чая и гири в 100 и 200 г . весы находятся в равновесии. Сколько граммов весит пачка чая?
2. Две одинаковые банки с вареньем и гиря в 5кг имеют ту же массу, что и 3 такие же банки и гири в 1кг и 2 кг. Какова масса банки с вареньем?
3. 3 одинаковых пакета с яблоками и 4 гири по 1 кг имеют ту же массу, что и 4 пакета с яблоками и гиря в 1кг. определи массу пакета с яблоками.
4. В 3 корзинах 18 кг винограда. Когда в одну корзину ещё 3 кг, во всех корзинах стало поровну. Сколько кг винограда было в каждой корзине первоначально?
5. За 1 кг конфет и 4 кг печенья заплатили 8 руб. 60 коп. Сколько стоит 1 кг конфет и 1 кг печенья, если килограмм печенья дешевле килограмма конфет на 1 руб. 10 коп?
6. На одной чаше весов находятся 5 пирожных, а на другой – 5 конфет и две гирьки по 200г. Сколько весит одна конфета и одно пирожное, если 10 конфет весят столько же, сколько два пирожных?
Рекомендуем посмотреть:
 Программа математического кружка 4 класс
Программа математического кружка 4 класс
 Решение нестандартных задач по математике в начальной школе
Решение нестандартных задач по математике в начальной школе
 Решение нестандартных задач по математике в начальной школе. Движение гусеницы
Решение нестандартных задач по математике в начальной школе. Движение гусеницы
 Задания для подготовки к олимпиаде по русскому языку, 3 класс
Задания для подготовки к олимпиаде по русскому языку, 3 класс
Похожие статьи:
Олимпиадные задания с ответами по математике для 1-4 классов
Олимпиадные задания по математике, 3 класс
Олимпиадные задания по математике, 4 класс
← Решение нестандартных задач по математике в начальной школе. Движение гусеницы | Сценарий прощания с 1 классом →
|
|
Автор: Елена Кряжевских
Опубликовано: 3760 дней назад (6 января 2014)
Просмотров: 30561
Блог: Блог Кряжевских Елены
Рубрика: решение олимпиадных задач
|
+3↑ Голосов: 3 |
| # 14 января 2014 в 15:06 +2 |
| # 14 января 2014 в 19:28 +1 | ||
|
| # 13 октября 2016 в 11:25 0 |
| Ошибка в первой задаче про 56 детей. 27+2=29, а не 39! |



