Коснпект урока информатики для студентов колледжа. Задачи оптимизационного моделирования

Разработка урока информатики для студентов колледжа

Тема урока: «Задачи оптимизационного моделирования в MS Excel»
Категория обучаемых: 2 курс, Группа 15ПГ1
Требуемый объем часов: 1 урока - 45 минут
Разработчик: Болотова О.Г., г.Пермь, 2016
Пояснительная записка
Данная разработка урока имеет большое значение в курсе «Информатики и ИКТ», так как она не только демонстрирует возможности информационных технологий – электронных таблиц, но и иллюстрирует моделирование экономических процессов.
При решении задачи, предложенном на этом уроке, осуществляется поиск наиболее оптимальных решений. Критерием оптимальности в задачах являются различные параметры: максимальное количество выпускаемой продукции, максимальная прибыль предприятия, минимальные затраты производства.
Разработанный урок содержит элементы развивающегося обучения, на последующем уроке отрабатываются элементы проблемного обучения (дополнительные задания), что способствует самостоятельной деятельности учащихся, развитию их мышления.
После данного урока учащимся для закрепления навыков предлагается самостоятельно выполнить ряд практических работ с оптимизационными задачами разного уровня сложности. Тем, кто недостаточно хорошо усвоил решение данного типа задач, предлагается задача, в которой рассматривается математическая модель этой задачи, остается только решить ее на компьютере. Для решения других задач учащимся необходимо самостоятельно разработать математическую модель и решить задачу на компьютере.
При изучении данной темы развиваются общие и профессиональные компетенции.
Общие компетенции:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, исходя из целей и способов ее достижения, определенных руководителем.
ОК 4. Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач.
Профессиональные компетенции:
ПК 2. Выполнять ввод цифровой и аналоговой информации в персональный компьютер с различных носителей.
В заключении урока учащиеся знакомятся с новым понятием из раздела математики – линейным программированием.

Изучаемые понятия:
• Оптимизационное моделирование;
• Алгоритм решения задач на оптимизацию;
• Надстройка «Поиск решения» в Excel.

План урока
• Организационный момент (2 мин)
• Актуализация знаний (12 мин)
• Работа на компьютере (27 мин)
• Подведение итогов урока (4 мин)

Цели урока:
• Научиться моделировать и строить задачи в среде MS Excel
• Составлять алгоритм решения задач на оптимизацию в среде MS Excel

Задачи:
Обучающие:
• Получение представления о решении задач на оптимизацию,
• Получение навыков работы с надстройкой «Поиск решения» в Excel,
• Выработка навыков работы с оптимизационными задачами в Excel.

Развивающие:
• научить использовать знания, полученные на уроках информатики, в профессиональной деятельности;
• развивать логическое мышление, умение обобщать, сопоставлять и применять полученные знания на практике;
• развивать познавательную деятельность учащихся, развивать умение анализировать происходящие изменения в решении задач;

• развивать познавательный интерес, творческую активность, интеллект;
• стимулирование познавательного интереса учащихся к данной теме и предмету “Информатика и ИКТ” в целом.
Воспитательные:
• профессиональная ориентация и подготовка к трудовой деятельности;
• подвести обучающихся к пониманию того, что от знаний, полученных на теории, зависит качество выполняемых работ на практике;
• развивать культуру общения, воспитывать внимание, сообразительность, находчивость.
Форма урока:
• Комбинированный (лекция и практическая работа за компьютером).

Материалы:
• Презентация на тему: «Задачи оптимизационного моделирования в MS Excel»
• Приложение 1. Текст конспекта.

Ход урока:
1. Актуализация знаний (повторение пройденного материала в форме диалога):
• Назначение MS Excel;
• Адресация ячеек;
• Диапазон ячеек;
• Ввод данных.
2. Введение в новый материал:
Табличный процессор MS Excel предоставляет пользователю большие возможности при решении различных расчетных задач. В нем имеется надстройка «Поиск решения», которая позволяет решать задачи отыскания наибольших и наименьших значений (наилучших) при заданных ограничениях.
3. Лекционная подача материала с конспектированием основных понятий (см. Приложение 1 и презентация).
4. Совместное решение задачи на компьютере (электронный документ Задача .xls и Приложение 2).
5. Закрепление пройденного материала (в форме общего обсуждения):
- Что мы понимаем под оптимизацией при решении определенного типа задач?
- Какую возможность табличного процессора MS Excel мы использовали при решении задачи на оптимизацию?
- Что необходимо задать, чтобы решить задачу с использованием надстройки «Поиск решения»?
- Можно ли добиться улучшения целевой функции, если – да, то как?
6. Заключение.
Достаточно часто при решении экономических задач требуется найти такие значения переменных, при которых целевая функция достигает максимального или минимального значения при заданных ограничениях. Решение таких задач удобно производить в MS Excel с использованием надстройки «Поиск решения». При решении данного типа задач строится математическая модель. Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием. А поскольку в целевую функцию переменные входят линейно, то данные задачи относятся к разделу этой науки, который называется линейным программированием.

Приложение 1
Решение оптимизационных задач в MS Excel
Оптимизационное моделирование – это поиск оптимального, т.е. наилучшего решения конкретной задачи при выполнении некоторых заданных условий.
Критерием оптимальности могут быть различные параметры, например, максимальное количество выпускаемой продукции, максимальная прибыль фирмы, минимальные затраты производства.
При решении задач оптимизационного моделирования на компьютере рекомендуется руководствоваться следующим алгоритмом:
1. Разобрать условие задачи.
2. На основе исходных данных построить математическую модель задачи:
- определить изменяемые (поисковые) переменные;
- задать ограничения;
- выбрать целевую функцию (критерий оптимизации). Целевая функция – это вещественная или целочисленная функция нескольких переменных, подлежащая оптимизации (минимизации или максимизации) в целях решения некоторой оптимизационной задачи.
3. Решить задачу на компьютере с помощью программы MS Excel.
4. Проанализировать полученные данные.

Перед началом работы в MS Excel необходимо убедиться, что надстройка «Поиск решения» установлена.
В Excel 2003: в меню «Сервис» имеется пункт «Поиск решения». Если его нет, нужно установить эту надстройку: в меню «Сервис» – «Надстройки» – устанавливаем флажок «Поиск решения».
В Excel 2007: «Данные» - «Анализ» - «Поиск решения». Если его нет, нужно установить. Чтобы активизировать ее в Excel 2007, щелкните значок Кнопка Microsoft Office , щелкните Параметры Excel, а затем выберите категорию Надстройки. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.
Рассмотрим решение задачи на оптимизацию на конкретном примере.
Задача.
Фирма "Компьютер-сервис" поставляет компьютеры под ключ четырех базовых комплектаций: "домашний", "игровой", "офисный" и "экстрим".
Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции.
Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.
Построим математическую модель решения данной задачи.
Пусть количество компьютеров каждого вида будут соответственно x1,x2,x3,x4?
Тогда общая прибыль = Прибыль за 1 ед.*количество модели
Прибыль = 33*x1+67*x2+110*x3+45*x4- Эта и будет целевой функцией.
Прибыль должна быть максимальной.
Итак, учитывая все условия задачи, приходим к ее математической модели: среди целочисленных решений системы линейных неравенств

Приложение 2
Решение задачи на компьютере.
1. Запустите MS Excel.
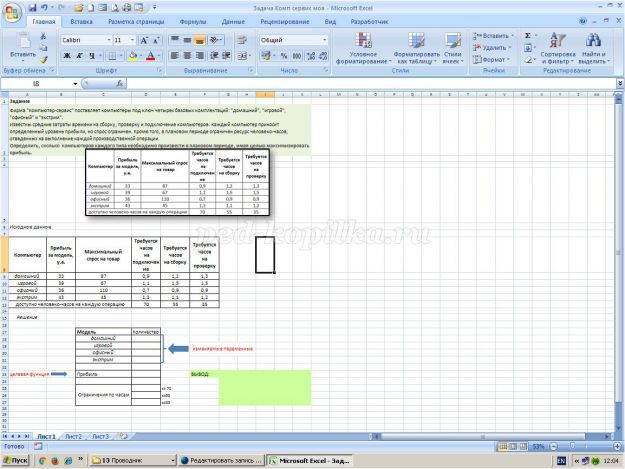
2. В новой рабочей книге на листе 1 заполните таблицу в соответствии с рисунком 1
В описанной модели необходимо максимизировать значение в ячейке D23. В качестве начальных значений принимаются количества информации и обозначаются x1,x2,x3,x4.
Ограничения задачи представлены в таблице 1:
Условие Ячейки
Ограничения по часам на подключение $D$25<=$D$13
Ограничения по часам на сборку $D$26<=$E$13
Ограничения по часам на проверку $D$27<=$F$13
Таблица 1
Дальнейшее решение задачи будем осуществлять с помощью надстройки «Поиск решения».
3. Выделите ячейку с оптимизируемым значением G6.
4. Выберите надстройку Поиск решения. Загрузится надстройка и появляется диалоговое окно «Поиск решения» (рис.2)
5. В поле «Установить целевую ячейку» уже находится ссылка на выделенную на предыдущем шаге ячейку (при необходимости эту ссылку можно изменить).
6. Установить переключатель «Равной» максимальному значению (ищется максимальное значение целевой ячейки G6).
7. Перейдите в поле «Изменяя ячейки:» и укажите диапазон ячеек, которые должны изменяться в процессе поиска наилучшего решения. В данном примере это ячейки $G$3:$G$4.
8. Щелкните по кнопке «Добавить», чтобы ввести первое ограничение задачи. Откроется диалоговое окно «Добавление ограничения» (рис.3).
9. Введите первое ограничение $D$18:$D$21>=0
10. Щелкните по кнопке «Добавить», введите следующее ограничение и т.д. из таблицы на предыдущей странице.
Примечание: для задания целочисленности значений ячеек в диапазоне $D$18:$D$21из второго раскрывающегося списка выберите «цел», при этом в поле «Ограничение» автоматически появится «целое». Какие еще ограничения присутствуют? Запишете их.
11. После ввода последнего ограничения нажмите ОК.
Окно поиск решения примет вид (рис.4)
Нажав на кнопку «Параметры можно проверить, и при необходимости, изменить условия и варианты поиска решения, что в нашей задаче не требуется.
12. Нажмите кнопку «Выполнить». По окончании поиска решения появится диалоговое окно результатов (рис.5).
13. Установите переключатель «Сохранить найденное решение», чтобы сохранить предложенные значения. С помощью этого диалогового окна можно также сформировать отчет.
14. Нажмите ОК. Получится решение
15. Напишите вывод.
16. Сохраните решение задачи в своей папке под именем Задача оптимазации.xls

Коснпект урока информатики для студентов колледжа. Задачи оптимизационного моделирования

Рекомендуем посмотреть: