Конспект урока информатики во 2 классе по теме: Объединение множеств

Урок изучения новой темы «Объединение множеств». В начале урока дается повторение предыдущего материала – пересечения множеств.
Цель урока: продолжение изучения операций над множествами, знакомство с понятием «объединения» множеств.
Задачи урока:
- образовательные: повторить пройденный материал с помощью игры «Назови пересечение»; закрепить умения использовать операции над множествами;
- развивающие: формировать у учащихся навыки работы с множествами;
- воспитательные: развивать познавательный интерес, творческую активность учащихся при выполнении заданий.
Тип урока: комбинированный (урок закрепления полученных знаний, изучение новой темы).

На уроке формируются универсальные учебные действия (УУД):
личностные: объяснять, что получается хорошо, что нет;
познавательные: наблюдать и делать самостоятельные выводы о главных признаках предметов и явлений;
регулятивные: определять цель деятельности; высказывать свою версию, пытаться предлагать способ ее проверки; определять успешность выполнения своего задания в диалоге с учителем, сравнивая результат с целью;
коммуникативные: оформлять свою мысль в устной речи, замечать различия своей и иной точек зрения, учиться выполнять различные роли в группе.

Программное обеспечение: ЦОР по информатике, 2 класс, Горячев А.В. «Информатика в играх и задачах»,
План урока
1. Организационный момент.
2. Повторение.
3. Игра «Назови объединение».
4. Игра «Пограничники».
5. Задание 73 в тетради.
6. Задание 74 в тетради (самостоятельно).
7. Игра «Сколько элементов?».
8. Задание 75 в тетради (самостоятельно)
9.Задание 76 в тетради.
10 Задание «Разные буквы».
11. Задание 78 в тетради.
12. Задача
13.Практическая работа за компьютерами
14. Оценивание учащихся.
15. Итоги урока.
16. Домашнее задание 79 в тетради. 1. Организационный момент.
2. Повторение.
2.1. Проверка домашнего задания 70 в тетради.
Вызывается один ученик к доске и разбирает домашнее задание.
2.2. Игра «Назови пересечение».
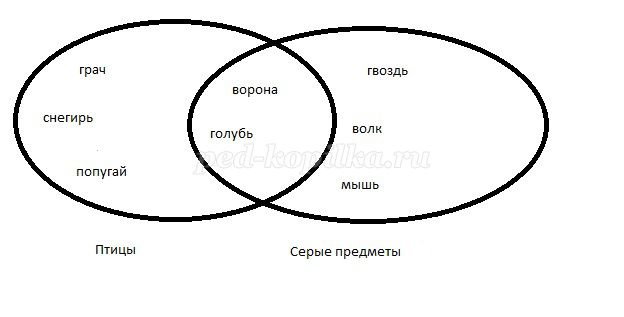
Учитель задает названия двух множеств, а ученики устно должны определить их пересечение и назвать как можно больше элементов этого пересечения. На доске вывешиваются картинки с изображением различных предметов, из которых нужно составить пересекающиеся множества.
Примеры:
- серые предметы и птицы (голубь, гусь, воробей и т.п.);
- овальные предметы и овощи (огурец, баклажан, кабачок, дыня и т.п.);
- металлические предметы и инструменты (нож, плоскогубцы, пила, гвоздь, винт и т.п.);
- ягоды и красные предметы (красная рябина и смородина, земляника, клубника, малина и т.п.).

3. Игра «Назови объединение».
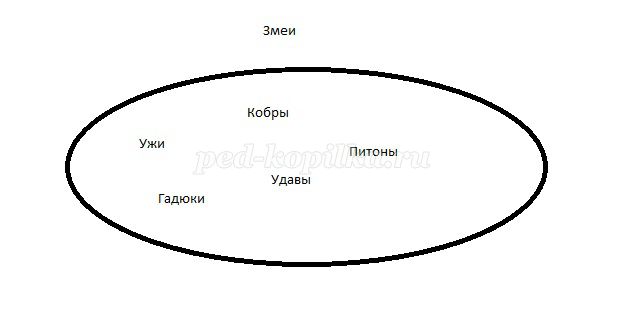
Учитель перечисляет множества, которые ученики должны объединить
в другое множество и назвать это множество. На доске вывешиваются картинки с изображением различных предметов, из которых составляются объединение множеств.
Примеры:
- ужи, гадюки, кобры, удавы ... - змеи;
- ромашки, розы, колокольчики - цветы;
- березы, дубы, осины, рябины - деревья;
- мальчики, девочки ... - дети;
- мамы, папы - родители;
- тигры, медведи, слоны, волки ... - звери;
- щуки, караси, акулы, окуни ... - рыбы;
- бабочки, жуки, кузнечики ... - насекомые.

4. Игра «Пограничники».
Проводится по трем следующим заданиям:
1) Задание 71 (а,б) в тетради.
а) Вызванный ученик рисует на доске требуемые множества в виде кругов.
б) Учитель: если теперь объединить эти множества в одно, то получим в данном случае все элементы обоих множеств. Такое множество называется объединением двух множеств (учитель заштриховывает на доске оба круга, а дети делают то же самое в тетради).

2) Задание 72 (а,б) в тетради.
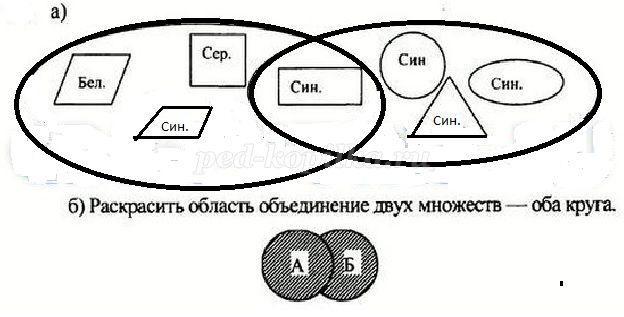
а) начало разбора аналогично предыдущему пункту. Но так как на вопрос:
«Может ли фигура быть одновременно и синей и четырехугольной?» учитель
должен получить утвердительный ответ, то на доске должны появиться два пересекающихся круга (множества). Заполнение кругов проходит по правилам игры «Пограничники»,
б) Учитель: Объединение этих двух множеств состоит из всех элементов обоих множеств, а их общие элементы входят в это объединение только по одному разу, так как в соответствии с пониманием множества в математике ни один элемент не может содержаться во множестве несколько раз (ведь он один!).

5. Задание 73 (а,б) в тетради.
а) С вызванным учеником учитель ведет диалог примерно следующим образом:
- Что такое прямоугольники? Это четырехугольники? (Да).
- А какие? (Особые. С прямыми углами.)
- А есть еще другие четырехугольники, без прямых углов (Есть. Ромб, трапеция, параллелограмм.)
- Значит, если ты - прямоугольник, ты всегда входишь в множество четырехугольников. Значит, эти множества ... (вложенные).
б) Учитель: Объединением этих множеств в данном случае будет само множество А (четырехугольников), так как прямоугольники итак входят в него.

6. Задание 74 (а,б,в,г) в тетради самостоятельно.
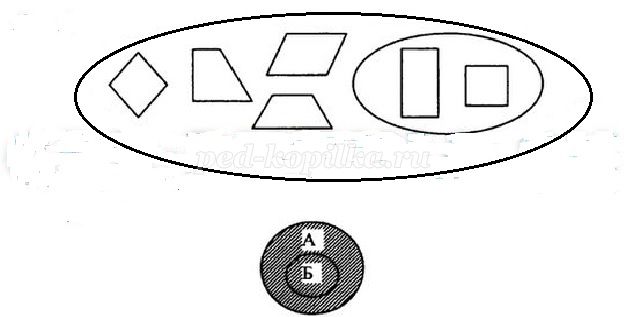
Аналогично пунктам 716, 726, 736 предыдущих заданий.
7. Игра «Сколько элементов?
а) Учитель просит встать всех девочек в классе (подсчитывает и записывает результат на доске). Затем просит встать всех мальчиков (результат подсчета записать на доске). Затем подсчитывается сумма и записывается на доске. И, наконец, просит встать всех мальчиков и девочек, т.е. объединение этих множеств (результат - подсчета на доске).
Оказывается, что сумма элементов двух множеств равна количеству элементов в их объединении.
б) Затем учитель просит встать девочек (результат - на доску) и девочек с косами (результат - на доску).
В данном случае в объединении элементов меньше, чем в сумме этих множеств.
в) Встают:
- девочки (подсчет - на доске, девочки садятся);
- дети в брюках (подсчет - на доске).
После подсчета суммы встают девочки и дети в брюках. И опять в объединении меньше элементов, чем в их сумме.
Учитель: А теперь разберемся, почему же в разных случаях результаты
различны.
а) Множество мальчиков и множество девочек.
Множества различны и поэтому объединение этих множеств равно сумме элементов двух множеств
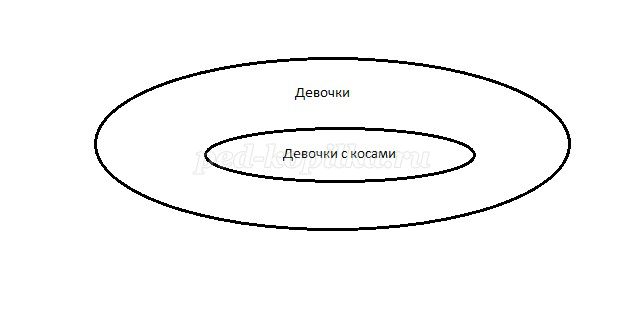
б) Девочки и девочки с косами.
В данном случае количество элементов в объединении равно количеству элементов в большом множестве (которое включает малое), То есть, меньше, чем простая сумма элементов этих множеств.
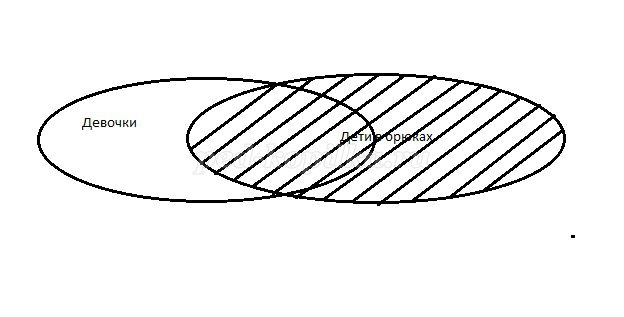
в) Девочки и дети в брюках.
В данном случае количество элементов в объединении немного меньше
суммы элементов обоих множеств, так как дети в брюках входят во множество девочек.

8. Задание 75 (а,б,в) в тетради (самостоятельно).
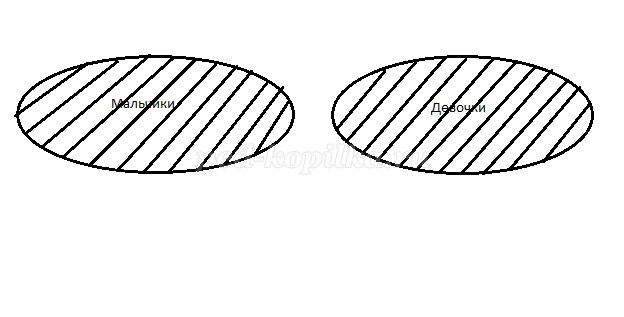
Аналогично предыдущей игре.
9. Задание 76 (а,б,в) в тетради.
После того, как дети подчеркнут требуемым образом предметы, они начинают выполнять пункты задания.
а) Напоминаю детям, что объединение множеств - это все элементы обоих множеств (без учета повторений). Значит, в наше объединение войдут все овощи и все красные предметы (т.е. как раз те предметы, которые мы подчеркнули, а помидор, подчеркнутый дважды, войдет только один раз).
б) Тот элемент, который остался не подчеркнутым, не принадлежит объединению.
в) Элемент, который подчеркнут дважды, принадлежит пересечению этих множеств, Т.е. входит в оба эти множества сразу.

10. Задание «Разные буквы».
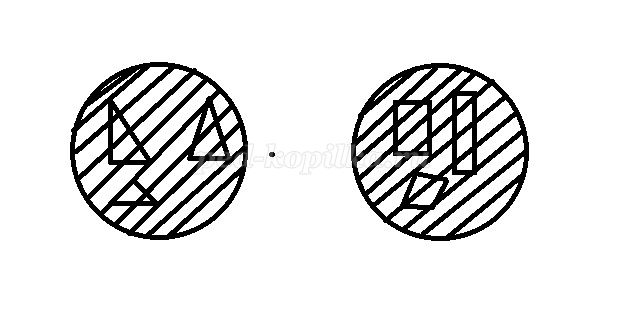
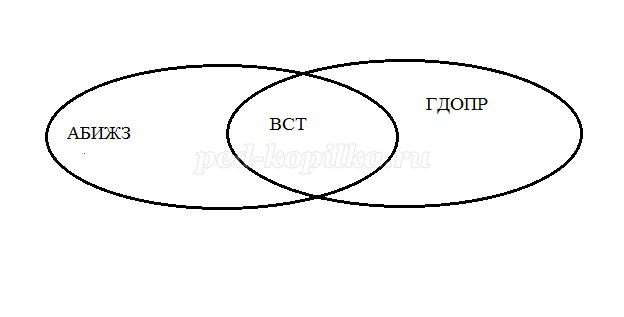
а) Учитель выписывает на доске несколько букв.
Например: АБВИЖЗСТ и ВГДОПРСТ.
Вопрос: Сколько всего разных букв написано на этих строчках?
У слышав ответ «16», учитель поясняет, что нас интересует не сколько всего
букв написано на обоих строчках, а сколько разных букв. И чтобы
подсчитать их количество составим схему в виде кругов.
Вопрос: А как расположены эти круги относительно друг друга? (Онь-
пересекаются, т.к. в этих множествах есть общие элементы (одинаковые
буквы).
После этого заполняются круги схемы. И по ней хорошо видно, что
разных букв на двух строчках всего 13.

11. Задание 78 в тетради (самостоятельно).
Решается аналогично предыдущему заданию.
12. Задача.
В объединении двух множеств 8 элементов, а в их пересечении 3 элемента. Сколько элементов может быть в этих множествах?
Раздаю детям 2 множества, они нарисованы на кальке овалами. Внутри множеств поставлены точками элементы: на 1 овале 4 точки и на 2 овале 4 точки. Так как множества пересекаются, то в их пересечении всегда будет 3 элемента. После этого останется 5 элементов, которые нужно «доложить» в эти множества следующими способами:
а) 1 и 4 (тогда в первом множестве будет 4 элемента, а во втором – 7);
б) 2 и 3 (в первом - 5, а во втором – 6);
в) 3 и 2 ( в первом – 6, во втором – 5);
г) 4 и 1 ( в первом – 7, во втором – 4)
Все это делаем накладывая один овал кальки на другой.

13. Практическая работа за компьютерами.
Ученикам нужно решить задания ЦОР к учебнику Горячева А.В. по теме «Объединение множеств».
14. Оценивание учащихся.
Учитель: Сегодня на уроке активно работал и много правильных ответов
дал(а) Оценка 5.
Остальных учеников оцениваю по выполнению заданий на компьютере.
15. Итоги урока.
Учитель: Итак, чему вы научились за сегодняшний урок?
Ученики: Узнали, что такое объединение множеств.
Учитель: А что такое объединение множеств?
Ученики: Все элементы, входящие в данное множество, называется
объединением данного множества. Если объединить несколько
множеств, то объединением будут все элементы этих множеств.
17. Домашнее задание.
Задание 79 в тетради.
Дети должны нарисовать множества в виде кругов (каких именно - они
должны решить сами), подписать их, а затем распределить фигуры по этим
кругам (указывая стрелочкой от фигуры к нужному кругу или рисуя фигуру в
нужном круге и вычеркивая ее из ряда).

Используемая литература
1. Горячев А.В., Горина К.И., Волкова Т.О. и др., «Информатика в играх и задачах» 2 класс. Изд. «БАЛАСС», 2014 г.
2. Горячев А.В. и др. «Методические рекомендации для учителя», 2 класс. Изд. «БАЛАСС», 2012 г.

Рекомендуем посмотреть:

Конспект урока информатики, 2 класс. Объединение множеств Урок информатики во 2 классе по теме: Объединение множеств