Урок информатики во 2 классе по теме: Объединение множеств

Урок изучения новой темы «Объединение множеств». В начале урока дается повторение предыдущего материала – пересечения множеств.

Цель урока: продолжение изучения операций над множествами, знакомство с понятием «объединения» множеств.
Задачи урока:
- образовательные: повторить пройденный материал с помощью игры «Назови пересечение»; закрепить умения использовать операции над множествами;
- развивающие: формировать у учащихся навыки работы с множествами;
- воспитательные: развивать познавательный интерес, творческую активность учащихся при выполнении заданий.
Тип урока: комбинированный (урок закрепления полученных знаний, изучение новой темы).
На уроке формируются универсальные учебные действия (УУД):
личностные: объяснять, что получается хорошо, что нет;
познавательные: наблюдать и делать самостоятельные выводы о главных признаках предметов и явлений;
регулятивные: определять цель деятельности; высказывать свою версию, пытаться предлагать способ ее проверки; определять успешность выполнения своего задания в диалоге с учителем, сравнивая результат с целью;
коммуникативные: оформлять свою мысль в устной речи, замечать различия своей и иной точек зрения, учиться выполнять различные роли в группе.
Программное обеспечение: ЦОР по информатике, 2 класс, Горячев А.В. «Информатика в играх и задачах»
План урока
1. Организационный момент.
2. Повторение.
3. Игра «Назови объединение».
4. Игра «Два города».
5. Объединение вложенных множеств.
6. Разместить элементы по множествам.
7. Игра «Сколько элементов?».
8. Задание «Разные напитки».
9. Работа в парах.
10.Практическая работа за компьютерами
11. Оценивание учащихся.
12. Итоги урока.
13. Домашнее задание 79 в тетради.

Ход урока
1. Организационный момент.
2. Повторение.
2.1. Проверка домашнего задания 70 в тетради.
Вызывается один ученик к доске и разбирает домашнее задание.

Ребята, вы помните Незнайку и его друзей - героев книг Николая Носова? Давайте сегодняшний урок проведем в сказочных городах, в которых был Незнайка и вспомним его друзей.

2.2. Игра «Назови пересечение».
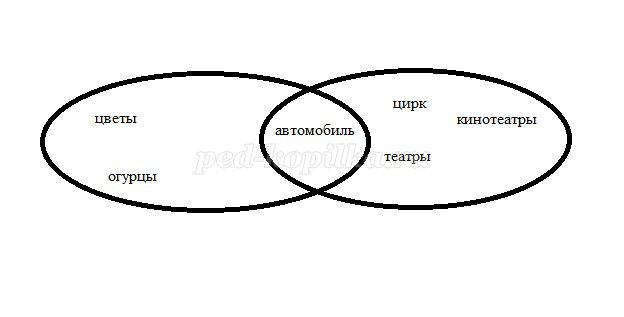
В Цветочном городе, в котором жил Незнайка, было много цветов, от чего он и назывался так. Сказочный город стоит на Огурцовой реке, названной так из-за произрастающих там в огромном количестве огурцов. В городе существовал автомобиль, работающий на газированной воде.
В Солнечном городе, в который в который Незнайка, Кнопочка и Пачкуля Пестренький совершили путешествие на газированном автомобиле, имеется зоопарк, цирк, множество театров, кинотеатров и спортивных площадок, Солнечный парк, архитектурное управление, фабрика модной одежды, научный городок. Большинство коротышек ездят на личных автомобилях.
Назовите пересечение этих множеств.

3. Игра «Назови объединение».
Незнайка, Знайка, Пилюлькин, Винтик, Шпунтик – это… (жители Цветочного города, персонажи, герои книги о Незнайке).
Цветочный, Солнечный – это… (сказочные города).
4. Игра «Два города».
Проводится по трем следующим заданиям:
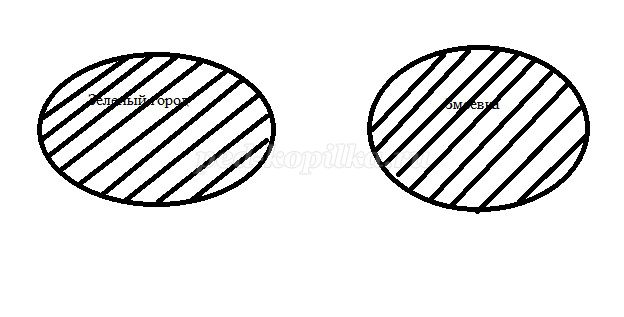
1) Зеленый город назван так из-за произрастающих там в большом количестве фруктовых деревьев. Город населён малышками.
Город Змеевка назван так из-за увлечения местных жителей — запуска воздушных змеев. Город практически лишён деревьев. В этом городе живут малыши.
а) Вызванный ученик рисует на доске требуемые множества в виде кругов.
б) Учитель: если теперь объединить эти множества в одно, то получим в данном случае все элементы обоих множеств. Такое множество называется объединением двух множеств (учитель заштриховывает на доске оба круга).

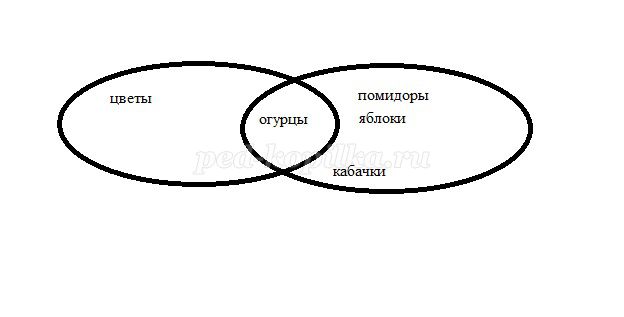
2) В Цветочном городе растет много огурцов, а в Зеленом городе Малышки занимаются тем, что выращивают овощи и фрукты.
а) Учитель: Что объединяет эти города? Огурцы, так как это овощи. Какие вы знаете еше овощи и фрукты? Давайте впишем, где они будут находиться. На доске должны появиться два пересекающихся круга (множества).
б) Учитель: Объединение этих двух множеств состоит из всех элементов обоих множеств, а их общие элементы входят в это объединение только по одному разу, так как в соответствии с пониманием множества в математике ни один элемент не может содержаться во множестве несколько раз (ведь он один!). Огурцы будут находиться только в пересечении!

5. Объединение вложенных множеств.
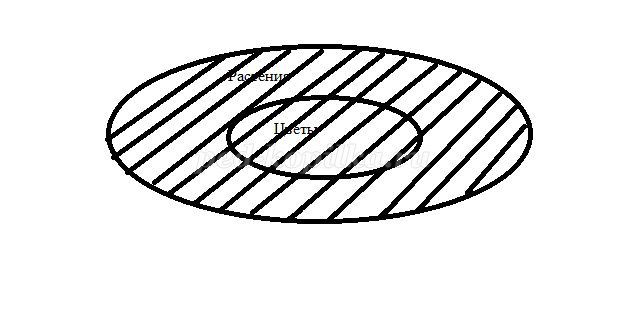
В Цветочном городе очень много различных цветов, а также возле него есть лес, в котором коротышки собирали грибы и ягоды. В лесу росли деревья: березы, сосны, ели, осины. На улицах Цветочного города росли цветы: колокольчики, маргаритки, ромашки, одуванчики. Какое множество будет растения, а какое – цветы? Расположите элементы внутри этих множеств.
а) С вызванным учеником учитель ведет диалог примерно следующим образом:
- Что такое цветы? Это растения? (Да).
- А есть здесь еще другие растения? (Есть. Березы, сосны, ели, осины.)
- Значит, если ты цветок, ты всегда входишь во множество растений. Значит, эти множества ... (вложенные).
б) Учитель: Объединением этих множеств в данном случае будет само множество растений, так как цветы и так входят в него.

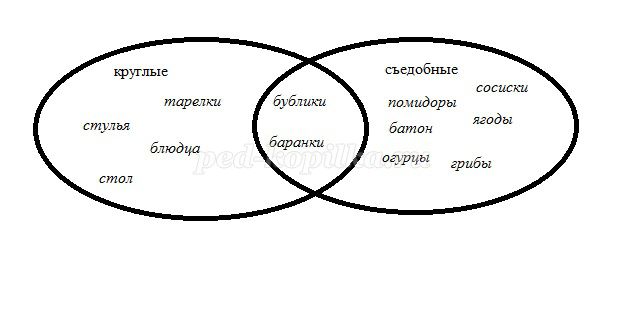
6. У Пончика в доме стояли круглые стулья, круглый стол, на котором лежали тарелки, блюдца. Пончик любил поесть, поэтому на столе, в тарелках и блюдцах у него лежали: сосиски, батон, бублики, баранки, помидоры, огурцы, грибы, ягоды. Разместите все эти предметы по множествам.

7. Игра «Сколько элементов?
Жители Цветочного города: Незнайка, Знайка, Гунька, Пилюлькин, Винтик, Шпунтик, Пончик, Авоська, Небоська, Кнопочка, Пачкуля Пестренький, Пулька, Сиропчик, Ворчун, Гусля, Капелька, Микроша, Молчун, Мушка, Растеряйка, Ромашка, Стекляшкин, Топик, Торопыжка, Тюбик, Цветик.
а) Девочки Цветочного города: Кнопочка, Капелька, Мушка, Ромашка. Остальные – мальчики. Подсчитываем сумму в этих двух множествах и записываем на доске. Оказывается, что сумма элементов двух множеств равна количеству элементов в их объединении.

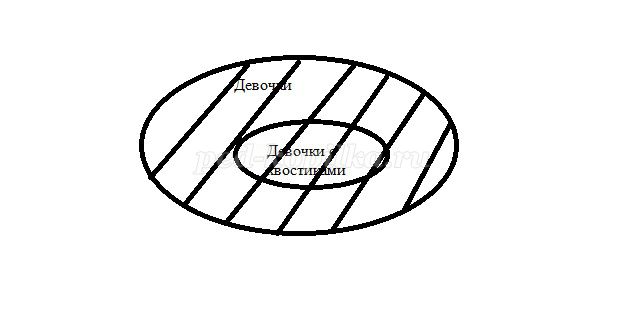
б) Из всех Девочек Цветочного города (результат - на доску) Ромашка и Кнопочка носили хвостики с бантиками (результат - на доску).
В данном случае в объединении элементов меньше, чем в сумме этих множеств.

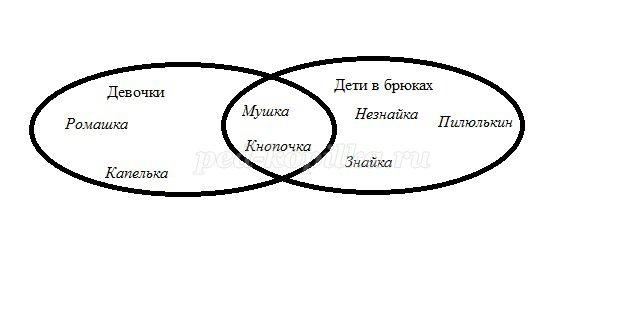
в) Мушка и Кнопочка иногда любили одевать яркого цвета брючки:
- девочки (подсчет - на доске);
- дети в брюках (подсчет - на доске).
И опять в объединении меньше элементов, чем в их сумме.

Учитель: А теперь разберемся, почему же в разных случаях результаты
различны.
а) Множество мальчиков и множество девочек.
Множества различны и поэтому объединение этих множеств равно сумме элементов двух множеств
б) Девочки и девочки с хвостиками.
В данном случае количество элементов в объединении равно количеству элементов в большом множестве (которое включает малое), То есть, меньше, чем простая сумма элементов этих множеств.
в) Девочки и дети в брюках.
В данном случае количество элементов в объединении немного меньше
суммы элементов обоих множеств, так как дети в брюках входят во множество девочек.

8. Задание «Разные напитки».
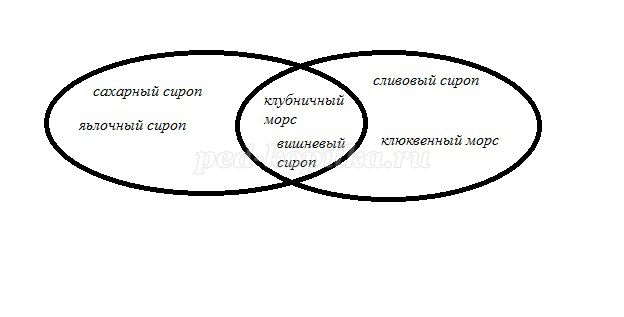
У Сиропчика дома стоят очень много различных бутылок с сиропами и напитками. На первой полке в буфете стояли бутылки с сахарным сиропом, с газированным сахарным сиропом, с клубничным морсом, с вишневым сиропом, с яблочным сиропом, с малиновым сиропом. На второй полке стояли клюквенный морс, вишневый сироп, грушевый сироп, клубничный морс, сливовый сироп, персиковый нектар. Сколько всего разных напитков стояло у Сиропчика в буфете?
а) Чтобы подсчитать их количество составим схему в виде кругов.
Вопрос: А как расположены эти круги относительно друг друга? (Они
пересекаются, т.к. в этих множествах есть общие элементы (одинаковые
напитки).
После этого заполняются круги схемы. И по ней хорошо видно, что
разных напитков на двух полках всего 9.

9. Работа в парах.
У Винтика и Шпунтика на двоих всего 8 различных деталей, 3 детали одинаковые. Сколько деталей может быть у Винтика и сколько деталей может быть у Шпунтика? 1 множество – детали Винтика, 2 множество – детали Шпунтика.
Раздаю детям 2 множества, они нарисованы на кальке овалами. Внутри множеств поставлены точками элементы: на 1 овале 4 точки и на 2 овале 4 точки. Так как множества пересекаются, то в их пересечении всегда будет 3 элемента. После этого останется 5 элементов, которые нужно «доложить» в эти множества следующими способами:
а) 1 и 4 (тогда в первом множестве будет 4 элемента, а во втором – 7);
б) 2 и 3 (в первом - 5, а во втором – 6);
в) 3 и 2 ( в первом – 6, во втором – 5);
г) 4 и 1 ( в первом – 7, во втором – 4)
Все это делаем, накладывая один овал кальки на другой.

10. Практическая работа за компьютерами.
Ученикам нужно решить задания ЦОР к учебнику Горячева А.В. по теме «Объединение множеств».
11. Оценивание учащихся.
Учитель: Сегодня на уроке активно работал и много правильных ответов
дал(а) Оценка 5.
Работа в парах: если все варианты нашли, то «5».
Остальных учеников оцениваю по выполнению заданий на компьютере.
12. Итоги урока.
Учитель: Итак, чему вы научились за сегодняшний урок?
Ученики: Узнали, что такое объединение множеств.
Учитель: А что такое объединение множеств?
Ученики: Все элементы, входящие в данное множество, называется
объединением данного множества. Если объединить несколько
множеств, то объединением будут все элементы этих множеств.
13. Домашнее задание.
Задание 79 в тетради.
Дети должны нарисовать множества в виде кругов (каких именно - они должны решить сами), подписать их, а затем распределить фигуры по этим кругам (указывая стрелочкой от фигуры к нужному кругу или рисуя фигуру в
нужном круге и вычеркивая ее из ряда).
Используемая литература
1. Горячев А.В., Горина К.И., Волкова Т.О. и др., «Информатика в играх и задачах» 2 класс. Изд. «БАЛАСС», 2014 г.
2. Горячев А.В. и др. «Методические рекомендации для учителя», 2 класс. Изд. «БАЛАСС», 2012 г.

Урок информатики во 2 классе по теме: Объединение множеств

Рекомендуем посмотреть:

Похожие статьи: