Восьмеричный переход
Описание работы: Данная разработка предназначена для учителей информатики и учащихся старшей школы. В ней рассматриваются некоторые способы решения задач на перевод чисел из одной системы счисления в другую. Один из способов решения задач – это комбинация нескольких переводов. Например, это может быть такой вариант: перевод из десятичной системы счисления в восьмеричную систему счисления, а затем перевод из восьмеричной системы счисления в двоичную. Во всех комбинациях переводов желателен переход к восьмеричной системе счисления.
Задача 1.
Представить десятичное число 607 в двоичной системе счисления.
Для перевода числа 607 в двоичную систему счисления используется способ, описанный в учебниках информатики. Он заключается в делении на 2 самого числа с получением частного и остатка, затем в делении всех получающихся частных также с получением остатков до тех пор, пока последнее частное не окажется равным 1. Цифрами двоичного числа становятся последняя единица, полученная как частное, и остатки от делений, выписанные в порядке, обратном их получению.
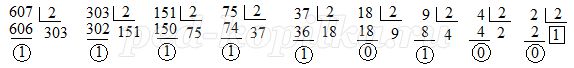 Рис. 1
Рис. 1
Это число 1001011111. Как видно из рисунка, здесь достаточно много делений. Гораздо быстрее такой способ. Вначале перевести число в восьмеричную систему счисления, а затем в двоичную.
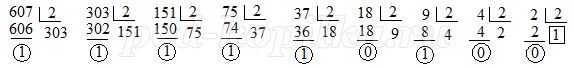 Рис. 2
Рис. 2
В восьмеричной системе счисления это будет число 1137. Заменяя каждую цифру восьмеричного числа тремя двоичными цифрами 001 001 011 111 согласно таблице 1, и отбрасывая два левых нуля, как незначащие, получим 10011111.
 Табл. 1
Табл. 1
Несомненно, что такую табличку необходимо либо помнить, либо воспроизводить по достаточно простому алгоритму на бумаге.
Третий способ заключается в разложении числа 607 на сумму степеней двойки с коэффициентами при степенях, равными либо 1, либо 0. Для этого нужно уметь воспроизводить табличку степеней двойки на бумаге либо хранить ее в уме. Максимальная степень двойки, которая имеется в числе 607 – это число 512 и она должна присутствовать в сумме с коэффициентом 1. Далее запишем в порядке убывания степени двойки 256, 128, 64, 32, 16, 8, 4, 2, 1. Вычитая из 607 число 512, получим 95. Значит, степени 256 и 128 могут присутствовать в сумме только с коэффициентом, равным 0, а степень двойки – число 64 с коэффициентом, равным 1. Далее, вычитая из 95 число 64, получим 31, откуда следует, что степень двойки – число 32 может присутствовать в сумме только с коэффициентом 0 и т.д. Таким образом, 607 = 1*512 + 0*256 + 0*128 + 1*64 + 0*32 + 1*16 + 1*8 + 1*4 + 1*2 + 1*1. Коэффициенты при степенях двойки, записанные подряд, образуют число 1001011111. Все три способа привели к одному и тому же двоичному числу 1001011111.
Задача 2.
Имеются 4 числа:
1) 101010111 - двоичное 2) 525 - восьмеричное 3) 345 - десятичное 4) 15D – шестнадцатеричное. Какое из них наименьшее?
Чтобы сравнить числа, представленные в разных системах счисления, надо получить их представление в одной системе счисления. Лучше всего выбрать для этого восьмеричную систему счисления. Для представления двоичного числа 101010111 воспользуемся таблицей 1. Начиная с младшего разряда, разобьём число на группы по три разряда и каждую группу заменим на одну восьмеричную цифру. Получим восьмеричное число 527. Теперь сравним это число с восьмеричным числом 525 из второго варианта ответа. Наименьшее из них – число 525. Чтобы представить десятичное число 345 в восьмеричной системе счисления, воспользуемся делением на 8. В результате первого деления получим первый остаток, равный 1, и частное, равное 43. При делении 43 на 8 получим второй остаток, равный 3, и частное, равное 5. Следовательно, десятичное число 345 в восьмеричной системе счисления – это число 531. Из всех трех восьмеричных чисел наименьшее - 525. Осталось сравнить его с шестнадцатеричным числом 15D. Для этого переведем число 15D в восьмеричную систему счисления следующим образом: вначале в двоичную систему счисления с помощью таблицы 2, заменяя каждую цифру числа четырьмя битами.
 Табл. 2
Табл. 2
Это будет двоичная последовательность 0001 0101 1101. Затем, отбрасывая три крайних левых нуля (они незначащие) и разбивая двоичное число 101011101 на тройки 101 011 101, заменим каждую тройку с помощью таблицы 1 одной восьмеричной цифрой, получим восьмеричное число 535. Из двух восьмеричных чисел 535 и 525 наименьшее число – 525. Таким образом, в качестве ответа задачи выберем второй вариант ответа.
Задача 3
Дано: восьмеричное число a = 233 и шестнадцатеричное число b = 9E. Какое из четырех двоичных чисел не принадлежит промежутку [a;b]?
1) 10011111 2) 10011101 3) 10011100 4) 10011011
Работая с таблицей 1, переведем двоичные числа в восьмеричную систему счисления: 1)237 2)234 3)236 4)233. Выстроим их в порядке возрастания: 233, 234, 236, 237. Поскольку речь в задаче идет только об одном числе, не принадлежащем промежутку [a;b], то, скорее всего, это будет число 237. Чтобы убедиться в этом, переведем шестнадцатеричное число b = 9E в восьмеричную систему счисления. Для этого переведем его вначале в двоичную систему счисления, используя таблицу 2. Это будет число 10011110. Затем получившееся двоичное число разобьём на группы по три разряда 10 011 110. Каждую группу по таблице 1 заменим одной восьмеричной цифрой. Получим восьмеричное число 236. Действительно только восьмеричное число 237 не принадлежит промежутку [a;b] и ответом задачи будет первый вариант двоичного числа из четырех, предложенных в задаче.
В данной задаче возможны и другие способы решения, например, перевод чисел a и b в двоичную систему счисления, а затем их сравнение с теми, которые имеются в ответе. Однако удобнее сравнение более коротких чисел. Можно было перевести все числа задачи в десятичную систему счисления, но в этом случае сам перевод чисел потребует выполнения достаточно большого количества вычислений.
 Что такое технология потоковых данных
Что такое технология потоковых данных
 Использование облачного хранилища данных в образовательном пространстве
Использование облачного хранилища данных в образовательном пространстве
 Конспект урока информатики по теме «Разветвляющие алгоритмы», 10 класс
Конспект урока информатики по теме «Разветвляющие алгоритмы», 10 класс
 Лабораторная работа по информатике для 5 класса на тему: Строение клавиатуры
Лабораторная работа по информатике для 5 класса на тему: Строение клавиатуры
Восьмеричный переход
В задачах ЕГЭ на работу с числами в различных системах счисления необходимо осуществлять перевод чисел из одной системы счисления в другую. Способы перевода известны, они описаны в учебниках по информатике. Однако экзамен ограничивает время на выполнение заданий. Чтобы выполнить задание не только правильно, но и быстро, необходимо научиться применять в каждом конкретном задании самые эффективные способы перевода чисел.Задача 1.
Представить десятичное число 607 в двоичной системе счисления.
Для перевода числа 607 в двоичную систему счисления используется способ, описанный в учебниках информатики. Он заключается в делении на 2 самого числа с получением частного и остатка, затем в делении всех получающихся частных также с получением остатков до тех пор, пока последнее частное не окажется равным 1. Цифрами двоичного числа становятся последняя единица, полученная как частное, и остатки от делений, выписанные в порядке, обратном их получению.
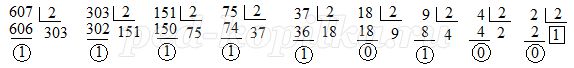
Это число 1001011111. Как видно из рисунка, здесь достаточно много делений. Гораздо быстрее такой способ. Вначале перевести число в восьмеричную систему счисления, а затем в двоичную.
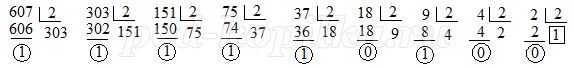
В восьмеричной системе счисления это будет число 1137. Заменяя каждую цифру восьмеричного числа тремя двоичными цифрами 001 001 011 111 согласно таблице 1, и отбрасывая два левых нуля, как незначащие, получим 10011111.

Несомненно, что такую табличку необходимо либо помнить, либо воспроизводить по достаточно простому алгоритму на бумаге.
Третий способ заключается в разложении числа 607 на сумму степеней двойки с коэффициентами при степенях, равными либо 1, либо 0. Для этого нужно уметь воспроизводить табличку степеней двойки на бумаге либо хранить ее в уме. Максимальная степень двойки, которая имеется в числе 607 – это число 512 и она должна присутствовать в сумме с коэффициентом 1. Далее запишем в порядке убывания степени двойки 256, 128, 64, 32, 16, 8, 4, 2, 1. Вычитая из 607 число 512, получим 95. Значит, степени 256 и 128 могут присутствовать в сумме только с коэффициентом, равным 0, а степень двойки – число 64 с коэффициентом, равным 1. Далее, вычитая из 95 число 64, получим 31, откуда следует, что степень двойки – число 32 может присутствовать в сумме только с коэффициентом 0 и т.д. Таким образом, 607 = 1*512 + 0*256 + 0*128 + 1*64 + 0*32 + 1*16 + 1*8 + 1*4 + 1*2 + 1*1. Коэффициенты при степенях двойки, записанные подряд, образуют число 1001011111. Все три способа привели к одному и тому же двоичному числу 1001011111.
Задача 2.
Имеются 4 числа:
1) 101010111 - двоичное 2) 525 - восьмеричное 3) 345 - десятичное 4) 15D – шестнадцатеричное. Какое из них наименьшее?
Чтобы сравнить числа, представленные в разных системах счисления, надо получить их представление в одной системе счисления. Лучше всего выбрать для этого восьмеричную систему счисления. Для представления двоичного числа 101010111 воспользуемся таблицей 1. Начиная с младшего разряда, разобьём число на группы по три разряда и каждую группу заменим на одну восьмеричную цифру. Получим восьмеричное число 527. Теперь сравним это число с восьмеричным числом 525 из второго варианта ответа. Наименьшее из них – число 525. Чтобы представить десятичное число 345 в восьмеричной системе счисления, воспользуемся делением на 8. В результате первого деления получим первый остаток, равный 1, и частное, равное 43. При делении 43 на 8 получим второй остаток, равный 3, и частное, равное 5. Следовательно, десятичное число 345 в восьмеричной системе счисления – это число 531. Из всех трех восьмеричных чисел наименьшее - 525. Осталось сравнить его с шестнадцатеричным числом 15D. Для этого переведем число 15D в восьмеричную систему счисления следующим образом: вначале в двоичную систему счисления с помощью таблицы 2, заменяя каждую цифру числа четырьмя битами.

Это будет двоичная последовательность 0001 0101 1101. Затем, отбрасывая три крайних левых нуля (они незначащие) и разбивая двоичное число 101011101 на тройки 101 011 101, заменим каждую тройку с помощью таблицы 1 одной восьмеричной цифрой, получим восьмеричное число 535. Из двух восьмеричных чисел 535 и 525 наименьшее число – 525. Таким образом, в качестве ответа задачи выберем второй вариант ответа.
Задача 3
Дано: восьмеричное число a = 233 и шестнадцатеричное число b = 9E. Какое из четырех двоичных чисел не принадлежит промежутку [a;b]?
1) 10011111 2) 10011101 3) 10011100 4) 10011011
Работая с таблицей 1, переведем двоичные числа в восьмеричную систему счисления: 1)237 2)234 3)236 4)233. Выстроим их в порядке возрастания: 233, 234, 236, 237. Поскольку речь в задаче идет только об одном числе, не принадлежащем промежутку [a;b], то, скорее всего, это будет число 237. Чтобы убедиться в этом, переведем шестнадцатеричное число b = 9E в восьмеричную систему счисления. Для этого переведем его вначале в двоичную систему счисления, используя таблицу 2. Это будет число 10011110. Затем получившееся двоичное число разобьём на группы по три разряда 10 011 110. Каждую группу по таблице 1 заменим одной восьмеричной цифрой. Получим восьмеричное число 236. Действительно только восьмеричное число 237 не принадлежит промежутку [a;b] и ответом задачи будет первый вариант двоичного числа из четырех, предложенных в задаче.
В данной задаче возможны и другие способы решения, например, перевод чисел a и b в двоичную систему счисления, а затем их сравнение с теми, которые имеются в ответе. Однако удобнее сравнение более коротких чисел. Можно было перевести все числа задачи в десятичную систему счисления, но в этом случае сам перевод чисел потребует выполнения достаточно большого количества вычислений.
Рекомендуем посмотреть:
 Что такое технология потоковых данных
Что такое технология потоковых данных
 Использование облачного хранилища данных в образовательном пространстве
Использование облачного хранилища данных в образовательном пространстве
 Конспект урока информатики по теме «Разветвляющие алгоритмы», 10 класс
Конспект урока информатики по теме «Разветвляющие алгоритмы», 10 класс
 Лабораторная работа по информатике для 5 класса на тему: Строение клавиатуры
Лабораторная работа по информатике для 5 класса на тему: Строение клавиатуры
Похожие статьи:
Оценка достижений учащихся на уроках информатики
Конспект открытого урока по информатике в 9 классе
Конспект урока информатики в 8 классе
|
|
Автор: Ирина Ивановна Биглова
Опубликовано: 4086 дней назад (17 января 2014)
Просмотров: 5475
Блог: Блог Бигловой Ирины
Рубрика: Методические разработки
|
+1↑ Голосов: 1 |
Нет комментариев. Ваш будет первым!



