Урок геометрии в 9 классе. Тема "Окружность. Круг. Длина Окружности". Конспект с презентацией

Тип урока: комбинированный урок.
Автор: Бердник Галина Станиславовна, учитель математики КОУ Ларьякской школы-интерната, для обучающихся с ОВЗ.
Представляю Вашему вниманию разработку урока по геометрии с презентацией. Материал будет полезен для учителей начальных классов.
Цель: Повторение понятия окружность и круг, их элементов, установление связи между ними; введение новых терминов; формирование умения проводить наблюдения и с помощью экспериментальных данных делать выводы; воспитание познавательного интереса к математике.
Личностные. Развитие навыка самостоятельности в практической деятельности, трудолюбия, аккуратности, пространственного воображения. Развивать творческую и мыслительную деятельность обучающихся, их интеллектуальные качества, интерес к математике.
Метапредметные. Формирование информационной, коммуникативной и учебной компетентности обучающихся; познавательного интереса в процессе ознакомления с историческим материалом, умения работать с имеющейся информацией в необычной ситуации.
Развитие коммуникативной компетенции обучающихся. Умение применять математические знания к решению задач. Демонстрация тесной связи геометрии с повседневной жизнью.
Воспитание интереса к геометрии, умение видеть математические задачи в окружающем нас мире.
Демонстрационный материал: циркуль, материал для опыта: предметы круглой формы и ленты, нитки (на каждого ученика), линейки; модель круга, цветные мелки.1. 1. Орг. момент.
Приветствие.
Проверка готовности к уроку.
Игра «Геометрический калейдоскоп»
- Кто сможет больше всех назвать геометрических фигур.
(Игра по цепочке, если ученик не может назвать фигуру, то он выбывает из игры)

2. Актуализация знаний.
- Фигура, о которой пойдет речь, была кем-то из вас озвучена.
- Прослушав информацию, догадайтесь, о какой фигуре пойдет речь.
«Древние греки считали эту фигуру совершеннейшей, безукоризненной, превосходной фигурой и «самой круглой».
+Окружность.
- Верно, замкнутая кривая линия, которая считается границей круга.
- В наши дни, в некоторых ситуациях, когда хотят дать особую оценку, используют слово круглый, которое считается синонимом слова полнейший.
Например, круглый отличник, круглый сирота. Что это значит?
- Как удобней и легче начертить окружность? (шаблон, циркуль)
- Само слово циркуль происходит от латинского «циркулюс» - круг, окружность. Сейчас уже нельзя сказать, кто именно изобрел этот инструмент - история не сохранила для нас его имя. Самый старый железный циркуль нашли во Франции. Он пролежал в земле более 2000 лет.
- С каким словом созвучно? «Цирк – циркуль «циркулюс» (круг). У цирка арена круглая, что представляется удобным для просмотра выступления артистов цирка.

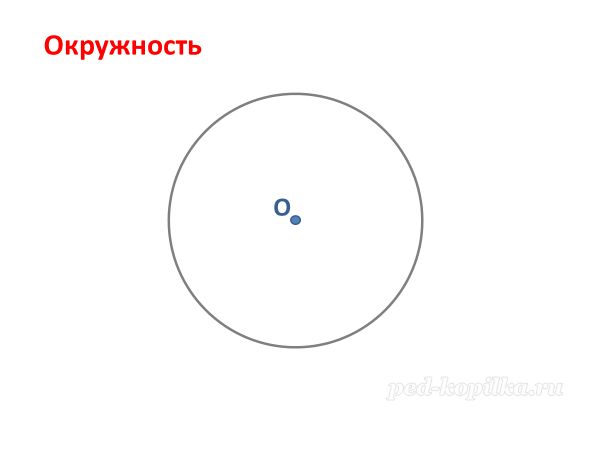
Практическая работа на альбомных листах.
ТБ с циркулем.
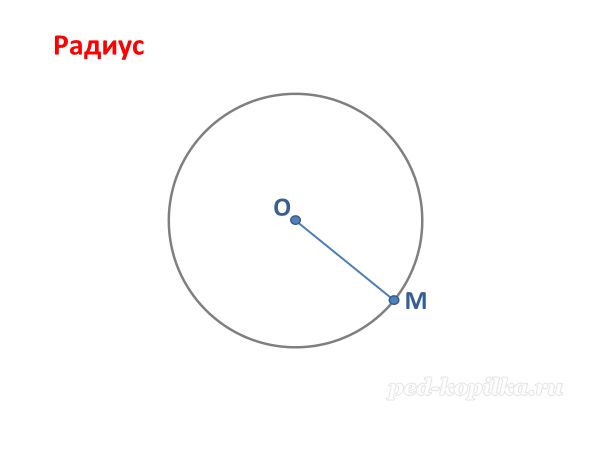
а) Начертить окружность радиусом 4 см (Обозначить центр окружности и радиус)
- Что такое радиус? Радиус лат. слово, в переводе на русский – луч, спица колеса.
+ Расстояние от центра, до любой точки окружности.

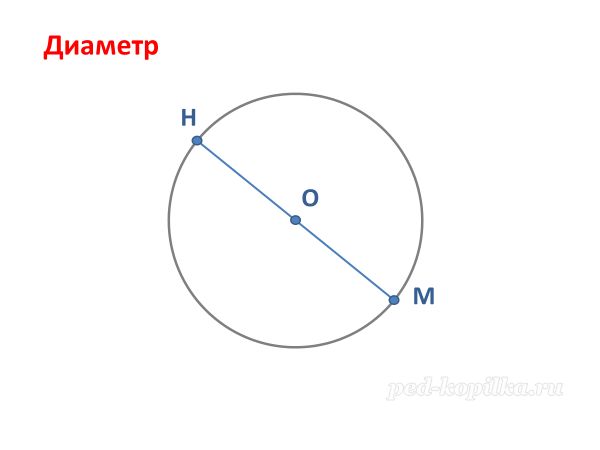
б) - Что такое диаметр? Диаметр греч. диа- насквозь, метр -мерить, измерять насквозь.
+ Отрезок, соединяющий две точки на окружности, который проходит через центр самой окружности. (начертить)

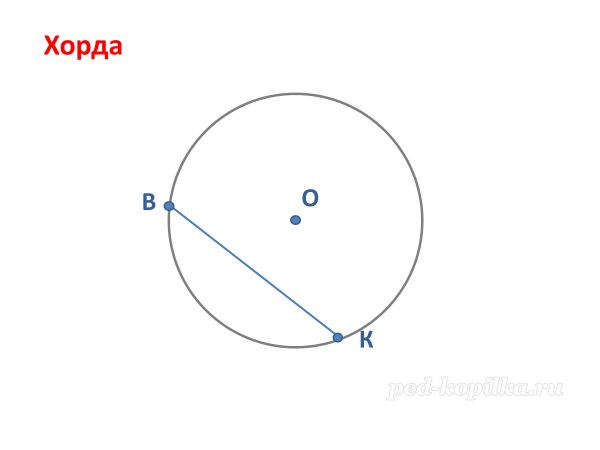
в) - Что такое хорда? (начертить) Хорда – греческое, в переводе на русский – струна.
+ Отрезок, соединяющий две любые ее точки. Диаметр есть самая длинная хорда.
- Сколько их можно провести?

г) - Если заштриховать внутреннюю часть плоскости, ограниченную окружностью, то получим геометрическую фигуру - круг.
«Общее свойство для окружности и круга - центр, радиус, диаметр, хорда"
Для общей информации: у круга есть ограниченная плоская поверхность, а значит можно найти площадь, есть сектор и сегмент.

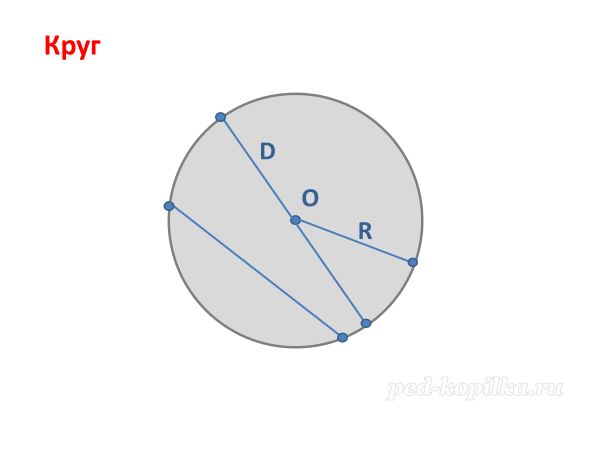
д) - Как определить диаметр в круге, если центр круга не определен? (показ)
(раздать круги из бумаги). Проверить путем сложения.
Также круг может являться шаблоном для черчения окружности.
е) Но, если нет циркуля и шаблона, как можно начертить круг на альбомном листе?
- Использовать диаметр окружности.
- Использовать скрепки.
3. Изучение нового материала.
- Знания, которые повторили и дополнили в первой части урока, пригодятся для изучения нового материала.
- Посмотрите на слайд, и скажите, могу ли я измерить длину ломаной, состоящей из нескольких отрезков? Как?
+ Измерить длину и сложить длину каждого отрезка.
- Как измерить длину кривой незамкнутой линии?
+ Выложить ниткой, вытянуть, измерить. (Можно использовать проволоку)
- Каким образом можно измерить длину круга (крышки, колеса, дна стакана)?
Работа в тетради.
- Есть несколько способов измерения длины окружности.
- Запишите в тетради тему урока "Длина окружности".
Способ 1. След от круга на прямой.
Учитель на доске чертит прямую, отмечает точку на ней и на границе модели круга. Совмещает их, а затем плавно катит круг по прямой до тех пор, пока отмеченная точка А на окружности не окажется на прямой в точке В. Отрезок АВ тогда будет равен длине окружности.

Способ 2. Можно сразу «прокатить» окружность вдоль линейки.
Ребята проводят исследование.
Лабораторная работа.
а) выполнить чертёж окружности, обведя дно пластикового стаканчика;
б) обернуть и измерить дно стаканчика лентой (примерно 13,3 см)
- Озвучьте результат. Это и есть длина окружности, обозначается буквой С (Ц э).
Запишите в тетрадь: С=13,3 см
- Однако такой способ измерения длины окружности неудобен, да и подручных средств может не оказаться. Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость. Сейчас мы в этом убедимся.
г) измерьте диаметр дна предмета линейкой (примерно 4,2см)
- Сравнивая полученные результаты, можем сказать, что диаметр примерно в три раза меньше длины окружности.
С примерно 13,3 см
Д примерно 4,2 см
С : Д примерно 3,1
- Действительно, при точных измерениях можно заметить, что каждый раз длина окружности примерно в 3,14 раза больше, чем диаметр окружности.

Эта зависимость была изучена в далекие времена в Древней Греции Архимедом.
Древнегреческий математик Архимед установил, что длина окружности относится к длине диаметра приближенно как 22:7
Обозначается Пи (греческая буква алфавита).
Если диаметр окружности обозначить буквой Д, а длину окружности С, то можно записать такую формулу
С примерно 3,14 · Д
Чтобы найти длину окружности, надо 3,14 умножить на длину ее диаметра.
Записать формулу в тетрадь.
Пи примерно 3,14159 –“ это я знаю и помню прекрасно”.
Пи примерно 3,14–“ это я знаю".
Физминутка.
- Чтобы верно выполнять задания по учебнику, не допускать ошибок, четко мыслить, выполним физические упражнения, связанные с нашей темой. Стоя у парты.
- Выполнить плавные круговые движения головой влево, вправо на счет1-4.
-Закинуть голову, начертить на потолке воображаемую окружность носом, радиус которой как можно больше. Опустить голову, начертить на полу воображаемую окружность.
- Повернуть голову, как можно дальше вправо (1-4), влево.
- Положить голову на правое плечо (1-4); левое плечо.
- Сделать глубокий вдох, задержать дыхание (1-4). Медленно выдохнуть. Сесть.
4. Работа по учебнику.
Стр.61 № 190
Стр. 62 № 192, 193
5. Итог урока.
- В чем отличие окружности от круга?
- Кто установил точное значение Пи
- Для чего нужно знать точную длину окружности?

Скачать эту презентацию

Рекомендуем посмотреть:

Конспект урока геометрии в 9 классе на тему: Предмет стереометрии. Многогранник Тест по итогам 1 четверти по математике в 9 классе Самостоятельная рабoта по геометрии, 9 класс. Преобразование фигур на плоскости Материалы для подготовки к ОГЭ 9 класс. Геометрия. Тема «Треугольник»