Математические игры для детей 1-2-3-4 класса

Дидактические игры с цифрами и числами для детей начальной школы

Игра 1

Учительница предлагает поочередно каждому из учеников угадывать образ тех чисел, которые она будет называть. Например:

Учитель называет цифры, а ученик называет соответственно образ, например:

5 — Отличник

10 — Футболист с мячом

2 — Лебедь

4 — Стул

0 — Бублик

Игра 2

Посмотрите внимательно на карточки, в которых нарисовано по 6 картинок. Каждая картинка — это образ цифры. Поставьте в пустых клеточках таблички, нарисованной с обратной стороны каждой карточки, вместо каждого образа числа, за которыми и закреплены соответствующие образы.

Игра 3

Придумайте коротенькую историю, например, как в мультфильме (можно смешную). Главными героями вашей истории должны быть образы заданных чисел.

Например, вам заданы цифры 7, 2, 10. Главными героями вашей истории являются образы этих чисел, а именно: пылесос, лебедь, футболист с мячом. Вам трудно связать героев в рассказ? Вот почитайте, как это делаем мы. У вас тоже все получится!

«Жили на свете друзья: лебедь, пылесос и футболист, у которого был мяч. Однажды футболист предложил своим друзьям поиграть в футбол. Долго над этим предложением хохотал лебедь:

— Да чем же наш пылесосик будет бить в ворота?

— А вот увидишь чем, — обиженно бурчал пылесосик. — У тебя хоть и лапки есть, да что толку! Они такие короткие. Да и вообще, кто в ластах в футбол играет?

— Разве можно друзьям ссориться! Давайте лучше начнем игру, а там и увидим, кто умеет играть, а кто нет! — вмешался футболист.

Друзья долго не раздумывали и тут же согласились. Каждому захотелось быстрее продемонстрировать свою скорость и ловкость.

Первым припустился лебедь со всех ног, да не успел. Смекалку пылесосик проявил: включился, притянул мяч к своему шлангу, а потом как выпустит воздух на него. И полетел мяч прямо в ворота.

Сел лебедь на траву, закрыл лапками глаза и горько заплакал от обиды. Подбежали к нему испуганные друзья, думали, он ушибся. Успокоили. Больше лебедь никогда ни над кем не смеялся».

Вот и придумали историю. Правда, легко? А теперь сами придумайте историю с главными героями на выбор:

5, 0,4

7, 3,9

1, 2, 3

4, 1, 0

3, 4, 8

6, 5, 10

2, 6, 7

8, 10, 1

10, 9, 2

9, 7, 5

0, 8, 6

Игра 4

Прочитайте внимательно и отгадайте — образы каких цифр участвуют в событиях историй?

История первая.

Присел усталый солдат на стул и, глядя в небо, задумался. Он мечтал скорее вернуться домой. Но его мечты прервало чье-то кряхтение. Очнулся солдат и стал внимательно осматривать территорию. Возле забора увидел он старичка, да такого усталого и голодного, что сердце его сжалось от боли. Солдат тут же посадил старика на стул и принес ему еды. Отдохнул старик, поблагодарил солдата и дальше пошел. А солдат устроился на стуле поудобнее и опять замечтался.

История вторая.

Весь вечер отличница ломала голову: «Как починить фары на папиной машине?» Хорошо, он пока не знал, что случилось, и было время все как следует обдумать. В голову ничего умного не приходило. Бедная отличница уже стала представлять, как завтра папа не сможет уехать на работу, станет выяснять, кто это сделал... А ей так не хотелось, чтобы взрослые ругали Юру Смирного из ее класса. Он такой хороший мальчик... да и попал камнем в машину ненарочно... Ну, так получилось! И вдруг ее осенило: «Точно, — решила она, — пойду рано утром, вкручу ему лампочку, повороты же будут работать, значит он может и не заметить...

История третья.

Как-то разговорились между собой лебедь и случайно пролетавшая птица.

— Да, — сказал лебедь, — везет же людям, у них есть машина, которая убирает жилье, ее пылесосом называют, — вот бы нам, птицам, такую?

— Интересная идея, — заметила незнакомка, — только для этого надо ее усовершенствовать.

— Как? — удивился лебедь.

— Как-как, — передразнила его незнакомка. — Мы же, птицы, летаем, вот и пылесос должен летать.

Следует отметить, что при выполнении задания (учащемуся, учителю или родителю) следует заносить результаты в рабочую тетрадь, так как контроль за качеством выполнения позволяет точно определить степень освоения школьником учебного материала. Для этого предлагается заполнять таблицу

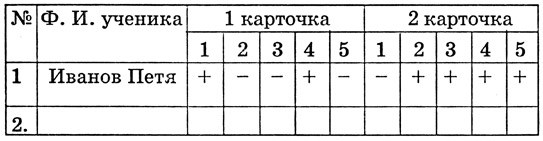
Таблица показана с примером ее заполнения. Упражнение считается отработанным, если оно многократно выполняется без минусов.

Ответ:

История первая: 1, 4, 9.

История вторая: 5, 6, 8.

История третья: 2, 3, 7.

Игра 5

(для первого класса)

Учитель раздает всем ученикам карточки, где возле цифр 1, 2, 3 написаны слова

Рекомендуем вырезать карточки из таблицы. При необходимости можно размножить на ксероксе нужное количество карточек.

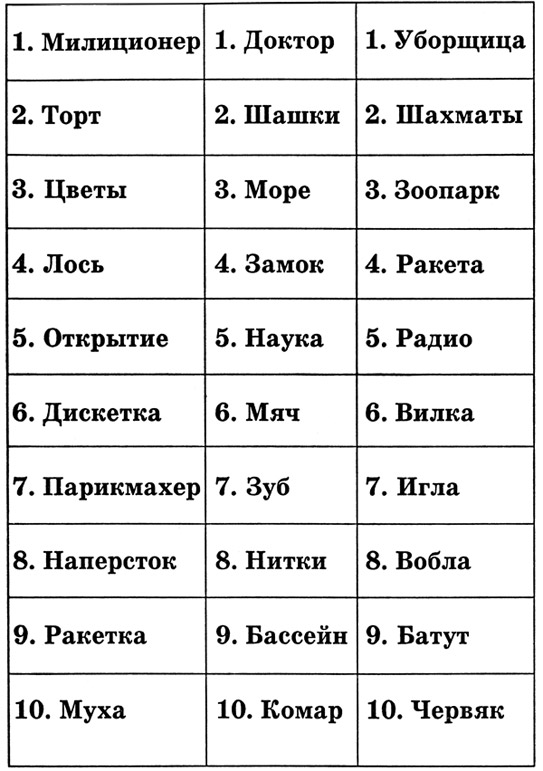
Задание. В течение всего пяти минут придумайте сначала первую историю, где главными героями будут являться: образ цифры 1 и образ слова, которое написано возле него. Под образом слова следует понимать то, что это слово обозначает в жизни. Например, по дороге бежит кошка, мы ее видим глазами — это живой образ слова «кошка». Потом придумайте вторую историю, где главными героями будут: образ цифры 2 и образ рядом стоящего слова. Затем следует придумать третью историю с главными героями: образ цифры 3 и образ рядом стоящего слова. Понятно? Начали!

Через пять минут учитель соберет карточки и попросит детей записать слова под номерами 1, 2, 3 в том же порядке, как было написано в карточке.

Следует отметить, что при выполнении задания (учащемуся, учителю или родителю) следует заносить результаты в рабочую тетрадь, так как контроль за качеством выполнения позволяет точно определить степень освоения школьником учебного материала. Для этого предлагается заполнять таблицу

Таблица показана с примером ее заполнения. Упражнение считается отработанным, если оно многократно выполняется без минусов.

Игра 6

(для первого класса)

Аналогична упражнению 5, но уже задается под пятью номерами по пять слов.

Время выполнения задания — 5 минут.

Игра 7

(для 2, 3, 4 классов)

Выполняется аналогично заданиям 4—5, но по карточкам с 7—10 словами в каждой. Время выполнения задания следует довести до 3 минут. Высоким результатом считается время 2 минуты. Карточки можно вырезать из таблицы

Игра 8

Запомните номера телефонов:

151-26-33,

365-85-84,

306-25-59,

238-12-48,

388-84-54,

307-43-12.

Для запоминания телефонных номеров следует использовать другой способ, а именно: образы цифр (слева направо) каждого телефонного номера в отдельности вы мысленно нанизываете на палочку. Вспомните эту игру, вы наверняка играли в пирамидку, когда были совсем маленькими, только тогда вы нанизывали колесики и шарики, а теперь вам надо нанизать образы цифр.

Посмотрите, как это делаем мы при запоминании телефонного номера 224-11-32.

Игра 9

Запомните 5 номеров телефона из любого телефонного справочника (таким образом, пусть первая цифра станет героем вашей истории, в которой он будет встречать образы последующих цифр и вступать с ними в какие-то взаимоотношения). Например, вам надо запомнить такой телефонный номер: 456-31-39. Образ цифры 4, то есть стул, становится главным героем вашей будущей истории, остальных героев он будет встречать по ходу продвижения по цифрам заданного номера телефона (соответственно, слева направо). Начали!

«В саду стоял стул и наслаждался природой. И вдруг на него как плюхнется отличник. Заскрипел стул, заохал. А отличник засиял от счастья, как лампочка. Ему-то хорошо, он набегался, и теперь есть где отдохнуть.

— Тьфу ты! — ворчал стул. — Ну что вот он... сначала чуть не сломал меня, а теперь пыхтит, как паровоз, отдышаться не может и не говорит ничего. Уж лучше бы села ко мне птица или солдат... Нет, лучше вместо солдата дедушка. С ними точно было бы интересно. Ведь птица высоко летает — много знает, а дедушка давно живет и мудро посоветовать сможет».

Игра 10

Попробуйте перевести на математический язык следующее сообщение:

«В корзине лежало 5 орехов. Из них два были плохими. Сколько орехов можно съесть?»

Игра 11

(для первоклассников)

Учитель пишет на доске: 5 + 3 = 8. Задает ученикам вопросы.

Вопрос 1. Что означает эта запись?

Вопрос 2. Придумайте задачу, которую можно решить с помощью такой записи.

На математическом языке такая запись называется «равенством» и переводится так: слева от знака «=» столько же, сколько и справа от знака «=». Можно изобразить это схемой:

В жизни такая запись напоминает весы.

Вес левой чаши равен весу правой чаши.

Ответ:

3 > 2

3 = 3

3 < 5

3 < 6

3 < 7

Игра 12

(для детей 6—7 лет)

Учитель рисует на доске весы (или вешает плакатик).

На левую чашу поставим гирю в 3 кг. Если на правую чашу положить:

2 (кг)

3 (кг)

4 (кг)

5 (кг)

6 (кг)

7 (кг)

На какой чаше тогда будет больше — в горошек или в клеточку? Как это записать математически, используя знаки «+», «-», «=», «<», «>»?

Как отличать математические знаки «<», «>». Запомните, к какому числу направлен острый нос, то число меньше.

Кого клюют — тот меньше!!!

Игра 13. Задача на смекалку

(для дошкольников и первоклассников)

Учитель пишет на доске равенство:

8 = 8

Слева от знака «=» стояла цифра 8, потому что в лесу жили 8 гномиков. К ним ворвались разбойники, забрали в плен 3 гномиков, вот так: 8-3.

Учитель пишет на доске:

8 - 3 = ?

Какая цифра будет теперь стоять справа?

Игра 14. «Лестница»

(для первоклассников)

Учитель выбирает 11 человек, каждый из которых берет в руки картонную карточку с одним из номеров от 0 до 10. Тот, кто получил соответствующий номер, как бы сам становится соответствующим числом. Дополнительно каждый участник игры получает по пять карточек — очков. Учитель объявляет: «Дети, сейчас мы будем играть в игру «Лестница». Что это за игра? Представьте себе, что я стою перед ступеньками лестницы. Ступеньки пронумерованы, и их всего 10. Нулевая ступенька — это земля. Первая стоит над землей, вторая — над первой, третья — еще выше, и так далее. А десятая ступенька завершает лестницу и стоит как бы на вершине горы. Сейчас я буду мгновенно оказываться на какой-нибудь ступеньке, а вы будете отгадывать — на какой. Только давайте договоримся. Если я говорю, что мне надо подняться на 2 ступеньки вверх, то вы прибавляете к номеру ступеньки, на которой я стою сейчас, число 2. А если я говорю, что мне надо спуститься на 1 ступеньку вниз, то вы, соответственно отнимаете от номера ступеньки, где я стою, единицу. Начнем?»

Учитель рисует на доске лестницу:

«Я стою на 4-й ступеньке. На какой ступеньке я окажусь, если мне надо спуститься на три ступеньки?»

Номер 1 поднимает вверх карточку с цифрой 1 и кричит: «Я!» Остальные молчат. Если номер 1 отгадал, ему за это присваивается «карточка-очко». У тех, кто неправильно назвал номер ступеньки, отбирается «карточка-очко».

Через пять ходов подсчитывается наличие карточек-очков у играющих, и в зависимости от этого детям выставляются отметки за участие в игре.

Одна карточка-очко соответствует единице. Две — двойке. Три — тройке. Четыре — четверке. Пять — пятерке. Оценки выставляются в журнал, а карточки передаются новым игрокам. Проведение первых трех игр должно быть пробным, то есть оценки в журнал не выставляются.

Игра 15. «Весы»

(для первого класса)

Учитель выбирает детей и присваивает им имена.

Первый — будет знаком «+». Ему на грудь прикрепляют большой картонный знак «+».

Второй — будет знаком «-». Ему на грудь прикрепляют знак «-».

Третий — будет знаком «=». Соответственно ему на грудь прикрепляют знак «=».

Еще 11 ученикам прикрепляются на грудь картонные кружки с числами, например, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Ученик со знаком «=» на груди встает посередине свободного пространства, вот так

Учитель договаривается с учениками, что все, происходящее слева от знака «=», он будет называть левой частью равенства, а справа от знака «=» — правой частью.

Каждому игроку и другим ученикам в классе раздаются карточки-очки.

Затем начинается игра.

Учитель, например, объявляет:

«В левой части появилась цифра 2. (Ученик с номером 2 бежит и занимает любое место с левой стороны от знака «=».) К цифре 2 в гости пришла цифра 1».

Учитель задает вопросы.

Вопрос 1. Как вы думаете, каким знаком обозначить слово пришел — знаком «+» или знаком «-»?

Тот, кто правильно отвечает, получает карточку-очко.

Тем временем цифра 1 и знак «+» занимают свои места рядом с цифрой 2, слева от знака «=», т. е. ученики с соответствующими картонными номерами на груди изображают равенство:

2 + 1 = 

Вопрос 2. Кто ответит, сколько цифр с левой стороны?

(Правильный ответ: две цифры.)

Вопрос 3. А если цифра 2 обозначает две конфеты, а цифра 1 — еще одну конфету, то сколько конфет слева от знака «=»?

(Правильный ответ: три конфеты.)

Та же самая игра повторяется в нескольких комбинациях, например:

1. В левой части появилась цифра: 5

К ней в гости пришла цифра «4», затем цифра «5», потом цифра «4» ушла. Сколько цифр осталось?

Ученикам предлагается обыграть цифры так же, как раньше учитель предлагал пример с конфетами.

(Вместо конфет можно использовать яблоки, игрушки и прочие предметы.)

2. В правой части появилась цифра: 5

В левой части стоит цифра 1

Вопрос. Какая цифра должна прийти к цифре 1?

Вариант. Весы в неравновесии (с теми же атрибутами)

Слева от знака «=» выстраиваются цифры таким же образом, как и в предыдущей игре (причем эти цифры приглашает учитель), а вот справа выстраиваются цифры, которые собирают ученики. Знак «=» должен ответить, имеет ли он право стоять на своем месте или должен уйти, т. е. равна ли сумма чисел слева от него сумме чисел, стоящих справа.

Например,

Дальше раздаются значки-цифры всем ученикам в классе (уже не по одному значку, а в определенном количестве). Количество значков, врученных ученикам, должно быть следующим:

1 — 10 штук

2 — 5 штук

3 — 3 штуки

4 — 2 штуки

5 — 2 штуки

Значки 6, 7, 8, 9 — по 1 штуке.

Игра проходит аналогично предыдущей, но условия слегка отличаются.

и так далее.

За правильные ответы выдаются карточки-очки, подводится итог, проставляются оценки.

Игра 16

(для 2—4 классов)

В этой игре, аналогичной предыдущей, ученикам, кроме значков от 0 до 9, раздаются несколько значков с числами 10 и 100 (не менее 9 значков 10 и не менее 5 значков 100 — можно больше, в зависимости от количества учеников в классе). Учитель приглашает учеников со значками для заполнения правой части равенства и ставит перед ними определенную задачу.

Например, предлагает ученикам пригласить в первую очередь «десятки» — максимально возможное их число, а потом остальные цифры.

1) 8 + 6 + 7 = 10 + 10 + 1

В уме ученики, решая эту задачу, должны сделать так:

8 + 6 + 7 =

8 + 2 + 4 + 7 =

10 + 4 + 7 =

10 + 1 + 3 + 7 =

10 + 1 + 10 =

2) 25 + 45 + 9 = 20 + 40 + 10 + 9

В уме ученики должны сделать так:

20 + 5 + 40 + 5 + 9 =

20 + 40 + 10 + 9

Та же игра проводится затем с сотнями.

Учитель предлагает ученикам пригласить в первую очередь «сотни» и «десятки» — максимально возможное их число, а потом остальные цифры.

3) 125 + 346 + 57 = 500 + 20 + 8

В уме ученики делают так:

100 + 20 + 5 + 300 + 40 + 6 + 50 + 7 =

400 + 20 + 40 + 50 + 10 + 8 =

Игра 17. Задачи на сообразительность

1) Через 5 лет Оле будет столько же лет, сколько ее брату Диме сейчас. Кто из них старше?

2) Через 6 лет Мише будет столько же лет, сколько Оле сейчас. Кто из них моложе?

3) Через 8 лет Саше будет на два года больше, чем Игорю сейчас. Кто из них старше?

4) Через 9 лет Инне будет на 12 лет больше, чем Сереже сейчас. Кто из них моложе?

5) Через 5 лет Даше будет на три года больше, чем Кате сейчас. Кто из них старше?

6) Через 6 лет Вите будет на 6 лет больше, чем Коле сейчас. Кто из них моложе?

7) Через 10 лет Гале будет на 11 лет больше, чем Ире сейчас. Кто из них старше?

8) Через 5 лет Максиму будет на 5 лет больше, чем Игорю через 5 лет. Кто из них старше?

9) Через 7 лет Насте будет на 7 лет больше, чем Свете через 7 лет. Кто из них моложе?

10) Через 10 лет Славе будет на 10 лет больше, чем Стасику через 8 лет. Кто из них старше?

11) Через б лет Грише будет на 6 лет больше, чем Толе через 8 лет. Кто из них моложе?

12) Через 12 лет Лене будет на 12 лет больше, чем Ире через 15 лет. Кто из них старше?

13) Через 8 лет Коле будет на 8 лет больше, чем Сереже через 6 лет. Кто из них старше?

14) Через 5 лет Тане будет на 5 лет больше, чем Вале через 3 года. Кто из них старше?

15) Когда Ире было 5 лет, ее младшей сестре Кате было два года. Сейчас Ира в два раза старше. Сколько лет Кате?

16) Сейчас Лене три года. Ее брат Саша старше ее на два года. Сколько лет будет Лене, когда брат будет в два раза старше, чем сейчас?

17) Когда моему отцу было 25 лет, мне было 6 лет. Сейчас отцу в два раза больше. Сколько мне лет?

18) Когда моему отцу было 25 лет, мне было 5 лет. Сколько лет будет моему отцу, когда я буду в два раза старше, чем сейчас?

19) У Пети, Саши, Вовы было два ранца и один портфель. У кого из мальчиков был портфель, если известно, что у Пети и Саши были одинаковые предметы?

20) У Марины, Кати и Нади было два набора красок и один набор цветных карандашей. Какой предмет был у каждой девочки, если известно, что у Кати и Нади были разные предметы?

21) У Саши, Игоря, Димы и Максима было три удочки и один спиннинг. Что было у каждого из них, если известно, что у Игоря и Саши были одинаковые предметы, а у Саши и Максима — разные?

22) У Гали, Иры, Кати и Даши было три пары туфель черного цвета и одна пара — белого. Какого цвета туфли были у каждой девочки, если известно, что у Иры и Кати туфли были одинакового цвета, а у Кати и Гали — разного?

23) У Володи, Миши, Кости, Саши и Саши было четыре набора шахмат и один набор шашек. У кого из них были шашки, если известно, что у Кости и Миши, а также у Кости и Саши были разные наборы игр?

24) У Маши, Лены, Кати, Лизы и Даши были четыре куклы и один медвежонок. Какая игрушка была у каждой девочки, если известно, что у Кати и Даши были одинаковые игрушки, а у Кати и Лизы — разные?

25) У Коли, Миши, Игоря, Вити и Сережи было три мороженых и два пирожных. Что было у каждого мальчика, если Коля и Миша купили одно и то же, Миша и Игорь — разное, Игорь и Витя — одинаковое?

Игра 18. Занимательное умножение

Некоторые особенности чисел находятся в прямой зависимости от принятой нами десятичной системы их обозначения. Они легко запоминаются, интересны и могут пригодиться для практических и теоретических приложений. К важнейшим из них относится сумма цифр всех чисел, получаемых в таблице умножения на 9.

Эти закономерности удобно использовать для запоминания таблицы умножения, а также для проверки правильности вычислений, предлагая ученикам после каждого выполнения умножения двузначных чисел на 9 найти сумму цифр полученного числа.

Существует еще несколько образчиков умножения, которые легко удерживаются в памяти благодаря своему внешнему виду:

* * *

* * *

Число, состоящее из всех значащих цифр, кроме 8, написанных в последовательном порядке, при умножении на 8, а также на 9 и числа, кратные 9 (18, 27, 36 и т. д.), дает интересные и легко запоминаемые результаты:

12345679 х 8 = 98765432

12345679x9 = 111111111

12345679 х18 = 222222222

12345679 х 27 = 333333333

12345679 х 36 = 444444444

12345679 х 45 = 555555555

12345679 х 54 = 666666666

12345679 х 63 = 777777777

12345679 х 72 = 888888888

12345679 х 81 = 999999999

Игра 19. Замечательные свойства «девяти»

(для 3—4 класса)

На интересных свойствах числа 9 очень часто основаны многие занимательные задачи и головоломки. Хорошо известно, например, что остаток, получаемый от деления любого числа на 9, всегда равен остатку от деления на 9 суммы цифр этого числа. Есть и другие занимательные свойства «девяти».

Например, нетрудно убедиться, что если мы напишем произвольное натуральное число, а затем запишем цифры этого числа в обратном порядке, то разность этих чисел всегда будет делиться на 9. Например: 72 - 27 = 45; 92 - 29 = 63 и т. д. Ясно, что (10а + b) - (10b + а) = 9 (а - b), т. е. всегда получается число, делящееся на 9. Вот примеры занимательных игр-головоломок, основанных на этом свойстве.

1) Задумайте любое двузначное число, переставьте в нем цифры и вычтите большее число из меньшего. Скажите мне только одну цифру полученной разности, и я скажу вам другую.

2) Задумайте и запишите число из трех цифр, разделите его на 9 и сообщите мне только остаток от такого деления. Зачеркните во взятом числе любую цифру (кроме нуля) и снова сообщите остаток от деления на 9 числа, полученного после зачеркивания цифры, тогда я сообщу вам зачеркнутую цифру.

Эти головоломки удобны для проведения викторин, конкурсов, КВН и т. д. Для проведения таких игр в классе одного из лучших учеников назначают ведущим, объяснив ему предварительно все секреты числа 9. Он дает задания остальным ученикам, а затем объясняет им секрет «фокуса».

Игра 20

В старинных итальянских рукописях встречается любопытный способ умножения многозначных чисел, который известен под названием мусульманского (или индусского) метода. Предположим, что нам надо перемножить числа 9347 и 258. Для этого начертите на бумаге в клетку три ряда по четыре клетки в каждом. Наверху напишите слева направо цифры множимого: 9, 3, 4 и 7, а слева снизу вверх цифры множителя: 2, 5 и 8. Проведя диагонали, как показано на рисунке, можете начинать умножение с любой цифры множимого на любую цифру множителя. Получающееся произведение (двузначное число) следует вписывать в соответствующий квадрат так, чтобы цифра десятков стояла в левом отделении квадратика, а цифра единиц — в правом. Когда все клетки окажутся заполненными, остается произвести сложение по направлению диагоналей. В нашем примере получается произведение 2411526 (читай слева направо и вверх).

В настоящее время для школьников этот метод представляет интерес как экскурс в прошлое.

Как складывать по диагонали:

Рассмотрим правый верхний квадрат. В нем как раз расположена первая диагональ, с которой и начинается подсчет суммы цифр по диагонали. Над первой диагональю лишь одна цифра 6, поэтому и результатом будет цифра 6. Над второй диагональю (т. е. ниже первой) цифры: 2, 5, 5. Их сумма равна 12. Два пишем в результате (2), а один оставляем в уме и переносим на сумму третьей диагонали и т. д.

Игра 21. Волшебная таблица

Предложите задумать любое число от 1 до 31, и пусть вам только укажут, в каких столбцах встречается задуманное число, и тогда вы имеете возможность безошибочно назвать его.

Например, вам скажут, что задуманное число находится в 1-м, 3-м, 4-м и 5-м рядах. Подумав несколько секунд, вы заявите, что задумано число 23.

Чтобы угадать задуманное число, которое находится, как вам сказали, в 1-м, 3-м, 4-м и 5-м рядах, сложите числа, стоящие в этих рядах снизу (набранные жирным шрифтом), то есть 1 + 2 + 4 + 16 = 23. Таким же образом можно указать любое другое число.

Игра 22. Загадочный календарь

Чтобы показать ребятам этот занимательный опыт, сделайте из фанеры или из картона круг, изображенный на рисунке. В центре круга укрепите гвоздем деревянную стрелку; она должна легко вращаться на оси — для этого наденьте на гвоздь маленькую шайбу. Чтобы стрелка останавливалась в любом положении, пропустите сквозь нее недалеко от острия куриное перышко так, чтобы, немного изогнувшись, оно упиралось в плоскость круга. При вращении стрелки перышко будет слегка тормозить ее движение.

На круге крупно напишите цифры. Названия месяцев, показанные на рисунке в скобках, писать не надо — они напечатаны только для того, чтобы вам было понятнее, как проходит опыт. Круг будет выглядеть более привлекательно, если вы несколькими штрихами нарисуете на нем забавную физиономию.

Повесив круг на классную доску или на щиток, вы обращаетесь к ребятам:

«Может ли кто-нибудь из вас быстро сказать, какой день недели будет через месяц или через полгода? Если у вас нет под руками календаря, то ответа на такой вопрос придется ждать довольно долго, и не всегда он будет верным. На доске вы видите простой прибор, с помощью которого я на подобные вопросы отвечаю быстро и безусловно правильно.

Возьмите у меня табель-календарь и проверьте, так ли это на самом деле. Скажите мне месяц и число по своему выбору, а я вам назову соответствующий день недели».

Когда кто-нибудь из зрителей, посмотрев на та- бель-календарь, задаст вам вопрос, вы сильно поворачиваете стрелку слева направо. Как только она остановится, вы безошибочно называете день недели. Табель-календарь подтверждает правильность вашего ответа.

Как же вы «угадываете» дни недели? В этом, конечно, вам помогает круг. Запомните, какое число на нем соответствует каждому месяцу года. Это совсем не трудно, если вы мысленно сравните круг с цифер- латом часов. Январю — первому месяцу года — соответствует число 7, написанное на круге в том месте, где на часах вы привыкли видеть цифру 1. На часах 2, а на круге 3; это число соответствует второму месяцу — февралю и т. д.

Когда вам называют месяц и число, вы, повернув стрелку, смотрите, какое число на круге соответствует месяцу. Это число вы складываете с числом, которое выбрано зрителем по табель-календарю.

К сумме надо прибавить число единиц в обозначении текущего года (для нынешнего года это будет 3). Результат сложения может быть меньше семи, или равен этому числу, или же, наконец, больше него.

В первом и во втором случае итог ваших вычислений соответствует дню недели, если принимать понедельник за 1, а воскресенье — последний день — за 7.

Если же результат сложения больше чем 7, то его надо разделить на это число. В таком случае может получиться остаток или его не будет. При делении нацело отгадываемый день — воскресенье. Во всех других случаях остаток соответствует дню недели:

1 — понедельник, 2 — вторник и т. д.

Примеры:

1. 1 мая. Маю — пятому месяцу — на круге соответствует 1. Число месяца первое (1 + 1 = 2). Год 1998 (2 + 3 = 5). Значит, отгадываемый день — пятница.

2. 1 августа (2 + 1 = 3; 3 + 3 = 6) — суббота.

3. 12 декабря (5 + 12 = 17; 17 + 3 = 20; 20:7 = 2, в остатке 6. Следовательно, 12 декабря 1998 года будет суббота.

4. 31 декабря (5 + 31 = 36; 36 + 4 = 39; 39 : 7 = 5, в остатке 4) — четверг.

Как видите, усвоив порядок очень простых арифметических действий, можно назвать любой день в году.

При чем же здесь стрелка, укрепленная на круге, и ее вращение? Пока стрелка движется, вы успеваете закончить необходимые вычисления. Ребята- зрители, естественно, думают, что отгадывание дней связано с вращением стрелкой. Такое убеждение складывается у них особенно легко потому, что вы каждый раз даете ответ, как только стрелка остановится.

Это позволяет скрыть от зрителей подлинные расчеты до конца опыта, когда вы должны объяснить его сущность своим товарищам.

Пусть те ребята, у которых нет табель-календаря, начертят у себя в записных книжках круг с числами, но, конечно, без стрелки. Пользуясь этим кругом, каждый, кто усвоит порядок вычислений, может без календаря определить название любого дня в году. Это бывает нужно во многих случаях.

Рекомендуем посмотреть:

Праздник по математике в начальной школе «Путешествие в страну Математики», 1-3 класс

Дидактические игры по математике, 1 класс

Сценарий математической сказки для начальной школы

Сценарий математической игры для 4 класса

Математические кроссворды и головоломки с ответами для 1-4 класса