Интеллектуальный марафон по математике с ответами, 5-9 класс

Интеллектуальный марафон (5-9 классы). Задачи и ответы

Интеллектуальный марафон - это вид соревнования, которое рассчитано на определенный срок.

Учащимся предлагаются задания в виде туров, даётся определенное время, в течение которого они выполняют задания и сдают решения учителям математики. Кроме задач предлагаются интересные сведения из истории математики. Подводятся итоги конкурса 2 раза в год. Решения заданий конкурса предлагаются через 2-3 тура.

I тур

Задача 1.

В соревнованиях по бегу участвовали 5 спортсменов. Василию не удалось занять I место. Сашу обогнал не только Дмитрий, но и еще один спортсмен, отставший от Дмитрия. Юра достиг финиша не первым, но и не последним. Сергей финишировал сразу вслед за Василием. Кто какое место занял в соревнованиях?

Задача 2.

Три друга - Витя, Коля и Петя - уехали отдыхать в лагерь, деревню и санаторий и занимались там волейболом, футболом и боксом.

Известно, что:

1) Витя уехал не в лагерь, а Коля - не в деревню.

2) В лагере нет секции бокса.

3) Тот, кто жил в деревне, занимался волейболом.

4) Коля не любит футбол.

Кто из товарищей и где занимается любимым видом спорта?

Задача 3.

Когда Ваню спросили, сколько ему лет, он подумал и ответил: «Я втрое моложе папы, но зато втрое старше своего брата Сережи». А маленький Сережа объяснил, что папа старше его на 40 лет. Сколько лет Ване?

Задача 4.

Тома «Детской энциклопедии» стоят в таком порядке: 1, 2, 6, 10, 3, 8, 4, 7, 9, 5. Как поставить их по порядку, если можно брать 2 соседних тома и ставить их, не меняя порядка, рядом на новое место (в начало, конец или между двумя томами)1

Задача 5.

В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какую из емкостей налита каждая жидкость?

Задача 6.

Петя, Гриша и Вася - неразлучные друзья. Их фамилии Лeпешкин, Ватрушкин и Бубликов. Однажды Вася с Гришей зашли к Пете домой. «Давайте решать шахматные задачи», - предложил Вася. Только приятели расставили шахматные фигуры, как в дверь постучали, и вошел почтальон. «Ватрушкину письмо!» - сказал он. Нам еще известно, что Лепешкин, решая задачу, предложил пожертвовать ладьей, с чем Вася не согласился и из-за этого чуть не поссорился с ним. Но Пете удалось примирить товарищей. Назовите фамилии Пети, Васи и Гриши.

Ответы на задачи I тура

Задача 1.

Ответ: Василий — IV место; Саша - III; Дмитрий — I; Юра — II; Сергей - V место.

Задача 2.

Ответ: Витя занимался волейболом в деревне; Коля - боксом в санатории; Петя - футболом в лагере.

Задача 3.

Чтобы узнать возраст Вани, нужно увеличить в 3 раза возраст Сережи или уменьшить в 3 раза число лет отца. Отсюда ясно, что отец старше Сережи в 9 раз, иными словами, разница между числом лет отца и Сережи равна возрасту Сережи, повторенному 8 раз. Значит, Сереже 5 лет, а Ване - 15 лет.

Задача 4.

Это можно сделать за 3 перестановки.

Условные обозначения:

• 6 10 - то, что взяли;

• 6 10 - где теперь находятся данные тома.

Задача 5.

Ответ: в бутылке - лимонад; в стакане - вода; в кувшине - молоко; в банке - квас.

Задача 6.

Ответ: Петя Ватрушкин; Гриша Лепёшкин; Вася Бубликов.

II тур

Задача 1. Логическая задача. «Три брата».

Три брата - Иван, Дмитрий и Сергей - преподают различные дисциплины (химию, биологию и историю) в различных университетах Москвы, Санкт-Петербурга и Киева. Иван работает не в Москве, Дмитрий работает не в Санкт-Петербурге. Москвич преподаёт не историю. Тот, кто работает в Санкт-Петербурге, преподаёт химию. Дмитрий преподаёт не биологию. Какой предмет и в университете какого города преподаёт Сергей?

Задача 2.

Разделите между тремя автомашинами 24 бочки бензина (из которых 5 полных, 11 полупустых и 8 пустых) так, чтобы на каждой автомашине оказалось одно и то же количество бочек и одно и то же количество бензина.

Задача 3.

Расстояние между двумя городами - 320 км. Из этих городов одновременно навстречу друг другу выходят два поезда. Один идёт со скоростью 45 км/ч, другой - со скоростью 35 км/ч. Вместе с первым поездом вылетает ласточка со скоростью 50 км/ч и летит навстречу второму поезду. Встретив этот поезд, ласточка поворачивает обратно и летит навстречу первому поезду. Встретив этот поезд, ласточка летит опять навстречу второму поезду и т. д. Какое расстояние пролетит ласточка, пока поезда не встретятся?

Задача 4.

По тропинке вдоль кустов

Шло 11 хвостов.

Сосчитать я также смог,

Что шагало 30 ног.

Это вместе шли куда-то

Петухи и поросята.

 

А теперь вопрос таков:

Сколько было петухов?

Мне б хотелось также знать:

Сколько было поросят?

Задача 5. Старинная восточная задача.

2 верблюда и 8 баранов стоят 18 таньга.

5 верблюдов и 2 барана стоят 27 таньга.

Сколько стоят отдельно верблюд и баран?

Задача 6.

Заполните пустые клетки таблицы так, чтобы сумма чисел в трёх соседних клетках (как по вертикали, так и по горизонтали) равнялась 12.

Ответы на задачи II тура

Задача 1. Логическая задача «Три брата».

Ответ: Сергей преподаёт биологию в Московском университете.

Задача 2.

5 полных бочек + 11 полупустых = 5-2+11=21 (полупустых бочек); 21 : 3 = 7 (полупустых бочек на 1 машину); 24 : 3 = 8 (бочек на 1 машину).

I вариант: 2 полных бочки, 3 полупустых, 3 пустых бочки; 2 полных, 3 полупустых бочки, 3 пустых; 1 полная бочка, 5 полупустых бочек и 2 пустых.

II вариант:3 полных бочки, 1 полупустая, 4 пустых бочки; 1 полная, 5 полупустых бочек, 2 пустых; 1 полная, 5 полупустых бочек, 2 пустых.

Задача 3.

Через 320 : (45 + 35) = 4 (часа) поезда встретятся; 50 · 4 = 200 (км) - пролетела ласточка.

Ответ: 200 км.

Задача 4.

7 петухов и 4 поросёнка.

Задача 5.

2 в. + 8 б. = 18 (таньга).

5 в. + 2 б. = 27 (таньга); умножим на 4 второе равенство и вычтем из него первое; получим: 20 в. -2 в. = 108 - 18; 18 в. = 90 таньга; 90 : 18 = 5 (таньга) - стоит 1 верблюд, 1 таньга - стоит 1 баран.

Ответ: 5 таньга стоит 1 верблюд, 1 таньга стоит 1 баран.

Задача 6.

III тур

Задача 1. Загадка принцессы.

По преданию, основательница чешского государства принцесса Либуша обещала свою руку тому из трёх женихов, кто сумеет решить задачу: «Если бы я дала первому жениху половину слив из этой корзины и ещё одну сливу, второму жениху - половину оставшихся слив и ещё одну сливу, а оставшиеся сливы поделила пополам и половину их и ещё три сливы дала бы третьему жениху, то корзина опустела бы». Сколько слив в корзине?

Задача 2. Крестьяне и картофель.

Шли 3 крестьянина, зашли на постоялый двор отдохнуть и пообедать. Заказали хозяйке сварить картофель, а сами заснули. Хозяйка сварила картофель, но не стала будить постояльцев, а поставила миску с едою на стол и ушла. Проснулся один крестьянин, увидел картофель и, чтобы не будить товарищей, сосчитал его, съел свою долю и снова заснул. Вскоре проснулся другой; ему невдомёк было, что один из товарищей уже съел свою долю, поэтому он сосчитал весь оставшийся картофель, съел третью часть и опять заснул. После чего проснулся третий; полагая, что он проснулся первым, он сосчитал оставшийся в чашке картофель и съел третью часть. Тут проснулись его товарищи и увидели, что в чашке осталось 8 картофелин. Тогда только прояснилось дело. Сосчитайте, сколько картофелин подала на стол хозяйка, сколько уже съел и сколько должен съесть ещё каждый крестьянин, чтобы всем досталось поровну?

Задача 3.

Стенные часы отбивают 6 ударов за 30 секунд. За сколько времени эти часы отобьют двенадцать ударов в полдень или в полночь?

Задача 4.

В школе зимой работали 3 спортивные секции - лыжная, хоккейная и конькобежная. В них занимались 38 человек. Известно, что в лыжной секции занимался 21 человек, среди которых 3 человека занимались ещё в конькобежной секции, 6 человек - ещё в хоккейной секции и 1 человек занимался одновременно во всех трёх секциях. В конькобежной секции занимались 13 человек, среди которых 5 человек занимались одновременно в двух секциях. Сколько человек занималось в хоккейной секции?

Задача 5.

Мишу спросили: «Три, три да три - что будет?» Он ответил: «Дыра». Это записали так: три + три + три = дыра. Какие цифры зашифрованы в этой записи, если одинаковые буквы обозначают одинаковые цифры, а разные буквы - разные цифры и известно, что (ы + ы): ы = ы?

Задача 6.

Муравьишка проехал на гусенице некоторое расстояние за 28 минут. За сколько минут муравьишка проедет на жуке расстояние в 4 раза большее, если скорость жука в 7 раз больше скорости гусеницы?

Ответы на задачи III тура

Задача 1. Загадка принцессы.

(([3 + 3 + 1]2+1) ·2) = 30 (слив) - было в корзине.

Задача 2.

1/3 - 1-й крестьянин; 1/3 · (1 - 1/3) = 2/9 - съел 2-й крестьянин; (1 - (1/3 + 2/9)) · 1/3 = 4/27 - съел 3-й крестьянин; осталось: (1 - (1/3 + 2/9 + 4/27)) = 8/27, что составляет 8 картофелин. 8 : 8/27 = = 27 (картофелин) - было. 1-й съел 9 штук; 2-й - 6 штук; 3-й - 4 штуки. 2-му надо съесть: 9-6 = 3 (картофелины); 3-ему надо съесть: 9-4 = 5 (картофелин).

Ответ: 27 картофелин подала хозяйка на стол.

Задача 3.

Если 6 ударов занимают 30 секунд, то значит, 1 удар от другого отделен паузой в 6 секунд. При 12 ударах таких пауз будет 11. Значит, бой часов в полдень или в полночь займет 66 секунд.

Задача 4.

16 человек занимались в хоккейной секции (7 + 3 + 1+5 = 16).

Задача 5.

403 + 403 + 403 = 1209.

Задача 6.

Если бы муравьишка проехал на жуке тот же путь, который он проделал верхом на гусенице, то он затратил бы на него в 7 раз меньше времени, то есть 4 мин (28 : 7 =4). Но на жуке он проехал расстояние в 4 раза большее, и, следовательно, на жуке муравьишка ехал 16 мин (4 · 4=16).

IV тур

Задача 1.

Из 100 студентов 28 человек изучают английский язык, 30 - немецкий, 42 - французский; 8 - английский и немецкий, 10 - английский и французский, 5 - немецкий и французский. Все три языка изучают 3 студента. Сколько человек изучают только один язык? Сколько студентов не изучают ни одного языка?

Задание 2.

Сквэрворд (square - квадрат, word - слово) - квадрат, разделённый на клетки, с написанными в нём определённым образом словами.

Расставить в оставшиеся клетки буквы из числа имеющихся (с, л, е, з, а) так, чтобы ни по вертикалям, ни по горизонталям, ни по большим диагоналям буквы не повторялись.

Задача 3.

Акробат и собачонка.

Весят 2 пустых бочонка.

Шустрый пёс без акробата

Весит 2 мотка шпагата.

 

А с одним мотком ягнёнок

Весит - видите - бочонок.

Сколько весит акробат

В пересчёте на ягнят?

Задача 4.

Вот задача не из лёгких!

Вычитай, дели и множь,

Плюсы ставь, а также скобки!

Верим, к финишу придёшь!

Употребляя цифру 7 по 4 раза, знаки действий и скобки, представьте все числа от 1 до 10 включительно.

Задача 5.

Медведь с базара плюшки нёс,

Но на лесной опушке

Он половину плюшек съел

И плюс ещё полплюшки.

 

Шёл, шёл, уселся отдохнуть

И под «ку-ку» кукушки

Вновь половину плюшек съел

И плюс ещё полплюшки.

 

Стемнело, он ускорил шаг,

Но на крыльце избушки,

Он снова пол-остатка съел

И плюс ещё полплюшки.

 

С пустой кошёлкою - увы!

Он в дом вошёл уныло...

Хочу, чтоб мне сказали вы,

А сколько плюшек было?

Ответы на задачи IV тура

Задача 1.

100 - (28 + 20 + 2 + 30) = 20 (человек) - не изучают ни одного языка; 13 человек изучают только английский язык; 20 человек - только немецкий; 30 человек - только французский язык.

Задача 2.

Задача 3.

Акр. + с. = 2 б.; с = 2 шп.; ягн. + шп. = б.; акр. + 2 шп. = 2 ягн. + + 2 шп.; акр. = 2 ягн.

Ответ: вес акробата равен весу двух ягнят.

Задача 4.

(7 + 7-7): 7 = 1;           (7*7 - 7):7 = 6;

7 : 7 + 7 : 7 = 2;           7 : (7 : 7) · 7 = 7;

(7 + 7 + 7) : 7 = 3;           (7 · 7 + 7) : 7 = 8;

77 : 7 - 7 = 4;            (7 + 7) : 7 + 7 = 9;

7 - (7 + 7) : 7 = 5;            (77-7):7=10.

Задача 5.

([0,5 · 2 + 0,5] · 2 + 0,5) · 2 = 7.

Ответ: было 7 плюшек.

V тур

Задача 1.

В трёх ящиках лежат орехи. В первом ящике на 6 кг орехов меньше, чем в двух других вместе. А во втором - на 10 кг меньше, чем в двух других вместе.

Сколько орехов в третьем ящике?

Задача 2.

Раздели 7 полных, 7 пустых и 7 полупустых бочек мёда между тремя купцами, чтобы всем досталось поровну и бочек, и мёда.

Задача 3.

Пароход проходит против течения путь от Астрахани до Казани за 6 суток, а от Казани до Астрахани (по течению) - за 4 суток. За сколько суток пройдут то же расстояние плоты, идущие сплавом?

Задача 4.

Расставьте числа в пустые клетки так, чтобы сумма любых трёх чисел подряд была одной и той же, а сумма всех чисел равнялась 200.

Задача 5.

Папу спросили, сколько ему лет. Он ответил, что сейчас ему вместе с мамой 55 лет, а 20 лет назад он был вдвое старше мамы. Сколько лет маме и папе?

Задача 6.

Ночь. Мальчик, мама, папа и бабушка находятся на одном берегу реки и хотят перейти по мосту на другой берег. Они имеют при себе один фонарик. По мосту могут идти максимум двое (обязательно с фонариком). Папа способен преодолеть мост за 1 минуту, мальчик - за 2 минуты, мама - за 5, бабушка - за 10 минут.

За какое наименьшее время они смогут переправиться на другой берег?

Ответы на задания V тура

Задача 1.

Соединим оба заданных условия и получим следующее утверждение: «В первом и втором ящиках орехов на 6 кг + 10 кг меньше, чем в первом, втором и двух третьих». Отсюда следует, что в двух третьих ящиках 16 кг орехов, то есть в третьем ящике

8 кг орехов.

Задача 2.

I вариант:

3 полных бочки, 1 полупустая, 3 пустых бочки;

3 полных бочки, 1 полупустая, 3 пустых бочки;

1 полная бочка, 5 полупустых, 1 пустая бочка.

II вариант:

2 полных бочки, 3 полупустых, 2 пустых бочки;

2 полных бочки, 3 полупустых, 2 пустых бочки;

3 полных бочки, 1 полупустая, 3 пустых бочки.

Задача 3.

Вниз по течению пароход проходит в сутки 1/4 всего пути, против течения - 1/6 часть. Разница равна 1/12 пути. Она равна удвоенной скорости течения реки. Поэтому течение проходит за сутки 1/24 всего пути от Казани до Астрахани. Значит, плоты пройдут этот путь за 24 суток.

Задача 4.

Задача 5.

Можно с уверенностью сказать, что и мама, и папа прожили по 20 лет, то есть в сумме 40 лет. Вычтя 40 лет из 55, узнаем, что 20 лет назад им было 15 лет. Значит, папе было 10 лет, а маме - 5 лет.

Ответ: папе - 10 лет, маме - 5 лет.

Задача 6.

Сначала идут мальчик и папа, затем папа возвращается (3 минуты), далее - мама и бабушка, мальчик возвращается (12 минут); затем папа и мальчик переходят на другой берег. Всего - 17 минут.

VI тур

Задача 1.

«Петя, почему ты не был у нас вчера? Моя бабушка праздновала свой день рождения», - сказал Коля. Петя спросил, сколько бабушке лет. Коля ответил: «Бабушка праздновала свой день рождения 15-й раз. Она его каждый раз празднует. Вот и сообрази, сколько бабушке лет».

Задача 2. Покупка сукна.

Некто купил 3/4 аршин сукна и заплатил за них 3 алтына.

Сколько надо заплатить за 100 аршин такого же сукна?

Задание 3.

Разрежьте квадрат на 5 прямоугольников так, чтобы никакие два прямоугольника не имели бы более одной общей вершины.

Задача 4.

Три друга - Витя, Коля и Петя - уехали отдыхать в лагерь, на юг и в дом отдыха и занимались там волейболом, футболом и боксом.

Известно, что:

1) Витя уехал не в лагерь, а Коля не на юг.

2) В лагере нет секции бокса.

3) Тот, кто живет на юге, занимается волейболом.

4) Коля не любит футбол.

Кто из товарищей и где занимался любимым видом спорта?

Задание 5.

Разрежьте фигуру на 8 равных частей.

Задание 6.

Расшифруйте запись:

Ответы на задачи VI тура

Задача 1.

Бабушка Коли родилась 29 февраля, ей исполнилось 60 лет. Разговор мальчиков происходил 1 марта.

Задача 2. Покупка сукна.

3/4 аршина стоят 3 алтына, значит, целый аршин стоит 4 алтына, то есть 12 копеек. А 100 аршин стоят: 12 · 100 = 1200 (копеек) = 12 рублей = 400 алтын.

Задание 3.

Задание 4.

Коля в доме отдыха занимался боксом, Витя (на юге) - волейболом, Петя (в лагере) - футболом.

Задание 5.

Задание 6.

90909+ 10101 = 101010.

VII тур

Задача 1. Десять замков.

В древности один правитель желал построить 10 замков, соединённых между собою стенами; стены должны были тянуться пятью прямыми линиями, с четырьмя замками на каждой линии. Приглашённый строитель представил такой план:

Но правитель остался недоволен этим планом, ведь при таком расположении можно подойти извне к любому замку, и ему хотелось, чтобы если не все, то хотя бы один или два замка были защищены стеной извне. Попробуйте найти такое решение, которое удовлетворяло бы требованиям правителя.

Задача 2.

Мышка ночью пошла гулять,

Кошка ночью видит - мышка!

Мышку кошка пошла поймать.

А вот перевод этого текста на языке племени Ам - ям:

Ам ту му ям

Ту ля бу ам

Гу ля ту ям.

Составьте словарь перевода с языка племени Ам - ям.

Задача 3. Как разделить орехи?

Говорит дед внукам: «Вот вам 130 орехов. Разделите их на 2 части так, чтобы меньшая часть, увеличенная в 4 раза, равнялась бы большей части, уменьшенной в 3 раза». Как разделить орехи?

Задача 4. Сколько весит рыба?

Хвост рыбы весит 4 кг, голова весит столько, сколько хвост и половина туловища, а туловище - столько, сколько голова и хвост. Сколько весит вся рыба?

Задача 5. Муха и два пешехода.

Два пешехода движутся навстречу друг другу по прямой дороге - каждый со скоростью 5 км/ч. Первоначальное расстояние между ними - 20 км. Муха, которая летает со скоростью 14 км/ч, взлетает с первого пешехода, летит по прямой ко второму, садится на него и, не теряя ни секунды, летит обратно к первому пешеходу, потом снова ко второму и т. д. Какое расстояние пролетит муха к тому моменту, когда два пешехода встретятся?

Ответы на задачи VII тура

Задача 1. Десять замков.

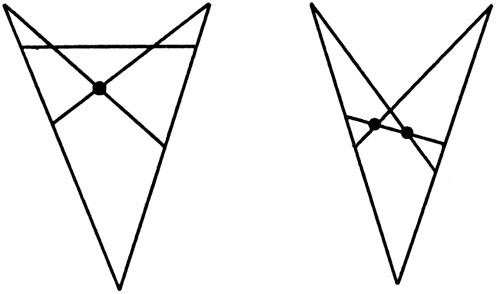
Задача 2.

Ту - мышка; ля - кошка; ам - ночью; пошла - ям; му - гулять; бу - видит; гу - поймать.

Задача 3. Как разделить орехи?

Уменьшив втрое количество орехов в большей части, мы получим их столько же, сколько их содержится в четырёх меньших частях. Значит, большая часть должна содержать в 3 · 4 = 12 (раз) больше орехов, чем меньшая. Поэтому меньшая часть должна содержать: 130 : 13 = 10 (орехов), а большая: 130 - 10 = 120 (орехов).

Ответ: 10 и 120 орехов.

Задача 4. Сколько весит рыба?

Туловище = голова + хвост; туловище = 0,5 туловища + 2 хвоста; значит, 0,5 туловища = 2 хвоста = 2 - 4 = 8 (кг). Вес туловища равен 16 кг, вес головы - 12 кг. Масса рыбы: 16 + 12 + 4 = 32 (кг)

Ответ: 64 кг.

Задача 5. Муха и два пешехода.

20 : (5 + 5) = 2 (часа) - идут пешеходы до встречи, и столько времени летит муха со скоростью 14 км/ч; 14 · 2 = 28 (км) - пролетит муха до встречи пешеходов.

Ответ: 28 км.

VIII тур

Задача 1.

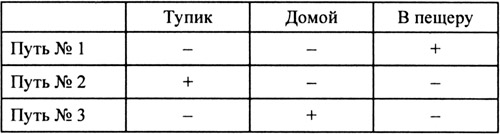
Дорога расходится в три стороны: домой, в тупик и в пещеру к Змею Горынычу. Около каждого пути стоит указатель и на нём написано:

«Путь № 1. Дорога в тупик».

«Путь № 2. Путь № 3 - дорога в тупик».

«Путь № 3. Дорога в пещеру».

Все знают, что надписи не соответствуют тому, что на них написано. По какому пути надо ехать, чтобы приехать домой?

Задача 2.

На первом этаже большого дома встретились 5 друзей. Женя сказал: «Если считать отсюда, то я живу выше, чем ты, Вова, в 2 раза, выше Пети - в 3 раза, выше Андрея - в 4 раза и выше Тани - в 6 раз». Андрей отозвался: «Это ты верно подметил. А ты, Петя, потише стучи, когда занимаешься гантелями у меня над головой».

На каком этаже живёт каждый из ребят?

Задача 3.

Том Сойер получил 4 алебастровых шарика и 1 яблоко за то, что дал товарищу покрасить 5 досок забора. 6 алебастровых шариков и 1 яблоко он получил за покраску 6 досок забора. Доски забора одинаковые. То же можно сказать о яблоках, а также о шариках. Затем он все яблоки обменял на шарики, а все полученные шарики отдал за ножик. Сколько шариков стоит ножик?

Задача 4.

Браун, Джонс и Смит - свидетели ограбления банка. Браун показал, что преступники скрылись на синем «Бьюике». Джонс утверждал, что это был черный «Крайслер», а Смит - что это был «Форд», но не синий. По рассеянности каждый из них указал правильно либо только марку, либо только цвет машины. На какой машине уехали преступники?

Задача 5.

Вася участвует в соревнованиях по бегу. В какой-то момент оказалось, что впереди него бежит одна треть всех участников, позади - половина всех участников, а рядом с ним никого нет. Сколько человек участвует в забеге?

Задача 6.

Старый гном разложил свои сокровища в 3 цветных сундука, стоящих у стены: в один - драгоценные камни, в другой - золотые монеты, а в третий - магические книги. Он помнит, что:

• красный сундук стоит правее, чем тот, где лежат драгоценные камни;

• магические книги правее, чем красный сундук.

В каком сундуке лежат магические книги, если зелёный сундук стоит левее, чем синий?

Задача 7.

Прямоугольный кусок волшебной кожи («шагреневая кожа») исполняет любые желания своего владельца, но после каждого исполнения желания он уменьшается на половину своей длины и на одну треть ширины. После исполнения 5 желаний он имел площадь 12 см2, а после двух желаний его ширина была 9 см. Какой была его длина после исполнения первого желания?

Ответ на задачи VIII тура

Задача 1.

Ответ: по пути № 3:

Задача 2.

Наименьшее число, делящееся на 2, 3, 4, 6, - это 12. Но если считать с 1-го этажа, то 2-му этажу соответствует 1 пролёт, 3-му - 2 пролёта лестницы, 4-му - 3 пролёта и т. д. Тогда Женя живёт на:

12 + 1 = 13 (этаже), Вова - на 12 :2+1 = 7 (этаже), Петя - на 12 : 3 + 1 = 5 (этаже), Андрей - на 12 : 4 + 1 = 4 (этаже), Таня - на 12 : 6 + 1 = 3 (этаже).

Задача 3.

4 ш. + 1 ябл. = 5 д.; 6 ш. + 1 ябл. = 6 д. Отсюда: 1 д. = 2 ш.,

1 ябл. = 5 · 2 - 4 = 6 ш.; значит, 1 ябл. = 6 ш.

Всего - 22 шарика.

Задача 4.

Чёрный «Бьюик».

Задача 5.

Все бегуны, кроме Васи, составляют вместе 1/2 + 1/3 = 5/6 всех участников забега. Значит, на долю Васи приходится 1/6 всех участников, то есть в забеге участвуют 6 человек.

Задача 6.

Сундуки расположены так: 3 - К - С; значит, магические книги (которые правее красного сундука) лежат в синем сундуке.

Задача 7.

Если в какой-то момент площадь шагреневой кожи равнялась S, то после исполнения очередного желания она станет равной: 1/2·2/3S, то есть уменьшится в 3 раза. После исполнения пятого желания площадь равнялась 12 см2, значит, после четвёртого желания она была равна: 12 · 3 см2, после третьего -12 · 9 см2, после второго -12 · 27 см2. Поскольку ширина в этот момент равнялась 9 см, то длина была 12 · 27/9 = 36 см. Значит, после первого желания длина кожи была 72 см, а ширина — 9 · 3/2 = 27/2 см (вариант 9 · 2 = 18 см для длины и 36 · 3/2 = 54 для ширины не подходит, так как 18 < 54).

Итак, после первого желания длина шагреневой кожи равнялась 72 см.

IX тур

Задача 1.

5 студентов стали победителями конкурса, набрав по 22, 21 и 20 баллов и заняв соответственно первое, второе и третье места. Сколько студентов завоевали каждое призовое место, если вместе они набрали 104 балла?

Задача 2.

Два муравья отправились в гости к стрекозе. Один всю дорогу прополз, а второй первую половину пути ехал на гусенице, что было в 2 раза медленнее, чем ползти, а вторую скакал на кузнечике, что было в 10 раз быстрее. Какой муравей первым придёт в гости, если вышли они одновременно?

Задача 3.

Сколько существует четырёхзначных чисел, которые делятся на 45, если две средние цифры у них 97?

Задача 4.

Найдите площадь треугольника, если площадь каждой клетки - 1 см2.

Задача 5.

Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал по 2 заявления:

• Браун: 1. Я не преступник. 2. Джонс - тоже.

• Джонс: 1. Это не Браун. 2. Это Смит.

• Смит: 1. Преступник Браун. 2. Это не я.

Было установлено, что один из них дважды солгал, другой дважды сказал правду, а третий один раз солгал и один раз сказал правду. Кто совершил это преступление?

Задача 6.

Два велосипедиста выехали одновременно из пунктов А и В навстречу друг другу и встретились в 70 км от А. Продолжая двигаться с той же скоростью, они достигли конечных пунктов и, отдохнув равное время, вернулись назад. Вторая встреча произошла в 90 км от В. Найдите расстояние от А до В.

Задача 7.

У первоклассника Феди в кассе цифр есть только единицы, четвёрки, шестёрки и девятки. Он составил из них 2 числа. Может ли одно из них быть ровно в 17 раз больше другого?

Ответы на задачи IX тура

Задача 1.

3 студента заняли 3 призовых места, набрав вместе 22 + 21 + 20 = 63 (балла). Значит, двое других набрали: 104 - 63 = 41 (балл). Значит, один набрал 21 балл, а другой - 20. Таким образом, они заняли соответственно второе и третье места. Значит, всего одно - первое, два вторых и два третьих места.

Задача 2.

Пока второй муравей ехал на гусенице полпути, а первый в это время полз в 2 раза быстрее, и, следовательно, прополз весь путь.

Задача 3.

Чтобы число делилось на 45, оно должно делиться на 5, то есть оканчиваться на 5 или 0, а также и на 9; значит, сумма цифр числа должна делиться на 9. Это числа 2970 и 6975.

Задание 4.

6 · 8 - 0,5 · (4 · 6 + 2 · 6 + 2 · 8) = 22 (см²).

Задача 5.

Преступником не может быть Джонс, так как иначе правдивые и ложные высказывания распределились бы так:

Браун: 1. Я не совершал преступления (правда). 2. Джонс тоже (ложь).

Джонс: 1. Это не Браун (правда). 2. Это Смит (ложь).

Это противоречит условию. Не может преступником быть и Смит, иначе дело обстояло бы так:

Браун: 1. Я не совершал преступления (правда). 2. Джонс тоже (правда).

Джонс: 1. Это не Браун (правда). 2. Это Смит (правда).

Это также противоречит условию.

Остаётся единственный вариант: преступник - Браун.

Браун: 1. Я не совершал преступления (ложь). 2. Джонс тоже (правда).

Джонс: 1. Это не Браун (ложь). 2. Это Смит (ложь).

Смит: 1. Преступник Браун (правда). 2. Это не я (правда).

Задача 6.

Общее расстояние, которое проехали оба велосипедиста до первой встречи, равно АВ, до второй встречи - 3АВ, поэтому от начала движения до второй встречи прошло в 3 раза больше времени, чем до первой. Велосипедист, который первоначально ехал из пункта А, проехал до первой встречи 70 км, следовательно, до второй встречи он проехал 210 км, причём из пункта В он проехал 90 км. Следовательно, расстояние от А до В равно АВ = 210 - 90= 120 (км).

Задача 7.

У него есть только 1, 4, 6, 9. Если число а заканчивается на 1, 4, 6, 9, то произведение числа а на 17 заканчивается на 7, 8, 2, 3. А таких цифр в кассе нет.

Х тур

Задача 1.

На столе поставлены в ряд бутылка минеральной воды, кружка, чашка, стакан и кувшин, причём в точно в таком порядке, в каком они перечислены. В них находятся различные напитки: кофе, чай, молоко, квас и минеральная вода, но неизвестно, какой напиток в какой посуде. Если стакан поставить между чаем и молоком, то по соседству с молоком будет квас, а кофе будет точно в середине. Определите, в какую посуду что налито.

Задача 2.

Дядя Федор (Ф), кот Матроскин (М), Шарик (Ш) и почтальон Печкин (П) сидят на скамейке. Если Шарик, сидящий справа от всех, сядет между дядей Федором и котом, то кот станет крайним слева. В каком порядке они сидят?

Задание 3.

Из шахматной доски вырезали 2 противоположные угловые клетки. Докажите, что оставшуюся фигуру нельзя разрезать на «домино» из двух клеток.

Задача 4.

На плохо отрегулированных весах бабушка взвесила 2 пакета сахарного песка - получилось 500 г и 300 г. Когда же она взвесила на тех же весах оба пакета вместе, то получилось 900 г. Определите по этим данным вес каждого пакета.

Задание 5.

Вставить в свободные клетки числа так, чтобы сумма чисел, стоящих в любых трёх соседних клетках, равнялась 20.

Задача 6.

В магазин привезли меньше 600, но больше 500 тарелок. Когда стали раскладывать их десятками, то не хватило трёх тарелок до полного числа десятков. Когда же стали раскладывать дюжинами, то осталось 7 тарелок. Сколько было тарелок?

Ответы на задачи X тура

Задача 1.

В кружке - чай, в чашке - молоко, в стакане - кофе, в кувшине - квас.

Задача 2.

По условию: М, Ш, Ф, П.

Задание 3.

Каждая клетка «домино» содержит 1 белую и 1 чёрную клетки. Но в нашей фигуре останется 32 белых и 30 чёрных клеток (или наоборот).

Ответ: нельзя разрезать домино из 2 клеток.

Задача 4.

Весы «уменьшают» вес каждого из взвешиваемых пакетов на 100 г.

Пакеты весят 600 г и 400 г.

Задание 5.

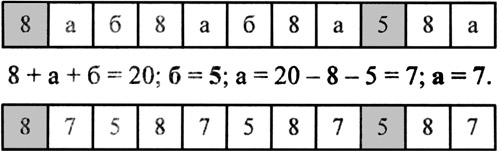
Задача 6.

Если не хватило трёх тарелок до полного числа десятков, то это значит, что, как и при счёте дюжинами, оставалось 7 тарелок. Значит, число тарелок без семи делится без остатка на 10 и на 12, то есть на 60. Среди чисел, меньших 600 и больших 500, только одно число 540 делится на 60; значит, число тарелок было: 540 + 7 = 547.

Ответ: 547 тарелок.

Рекомендуем посмотреть:

Игровая программа по математике, 5 класс

Задачи на «Инвариант» с ответами, 6 класс. Алгебра

Математическая игра «Поле чудес» для 6 класса

Математический бой, 5 класс. Задания с ответами

Олимпиадные задачи на тему «Чётность» с ответами, 5 класс