Устный журнал «Пифагор и его школа» для школьников 7-8 классов
Цели: познакомить учащихся с жизнью и творчеством Пифагора Самосского; расширить знания учащихся по данной теме.
Оформление: карта Древней Греции, портрет Пифагора, египетский треугольник (веревка с узлами), рисунок, иллюстрирующий один из способов доказательства теоремы Пифагора.
Ход устного журнала
I. Организационный момент.
Учащиеся садятся за столы по классам, получают чистые листы и ручки.
II. Презентация устного журнала.
Учитель. Сейчас состоится презентация устного журнала «Пифагор и его школа».
«Репортеры» будут делать сообщения, цель которых - знакомство с жизнью и деятельностью Пифагора. Но страницы журнала должны быть проштудированы всеми «читателями», а для этого: внимание! «Пролистывая» текст, вы должны сформулировать вопросы для команд - «соперниц» по материалу данной странички.
Страница первая «Пифагор и его школа».
1. Жизнь Пифагора на родном острове Самосе.
2. Пифагор - основатель пифагорейской школы.
Страница вторая «Числа правят миром».
1. «Божественные» числа: линейные, плоские, треугольные числа.
2. Пифагоровы тройки.
3. Иррациональные числа.
Страница третья «Теорема Пифагора»
1. «Теорема невесты».
2. «Пифагоровы штаны».
3. Стихи о Пифагоре.
III. Заключительное слово учителя.
Смерть Пифагора также окружена красивыми легендами. По одной из них, дом в Кротоне, где Пифагор собирался со своими учениками, был подожжен. Преданные друзья бросились в огонь и проложили в нем дорогу учителю, чтобы он по их телам вышел из огня, как по мосту. Друзья погибли, а сам Пифагор, будучи спасенным такой дорогой ценой, так затосковал, что лишил себя жизни. Умер Пифагор около 500 г. до н. э.
Пифагорейская школа после смерти учителя продолжала существовать и действовать еще в течение нескольких сот лет.
Слава Пифагора разошлась по всей Греции и Древнему Риму. Даже противники признавали гениальность Пифагора. Рассказывают, что в Риме была поставлена статуя Пифагору - «самому мудрому из греков».
Приложения
Приложение 1
Жизнь Пифагора
Пифагор не только самый популярный ученый, но и самая загадочная личность, человек-символ, философ, пророк.
Подлинную картину его жизни и достижений восстановить трудно, так как письменных документов о Пифагоре Самосском не осталось.
Известно, что Пифагор родился на острове Самос в Эгейском море у берегов малой Азии около 570 г. до н. э. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и незаурядные способности. Увлекался музыкой и поэзией. Неугомонному воображению Пифагора очень скоро стало тесно на маленьком острове! Мудрый Ферекид - один из учителей Пифагора - однажды сказал: «Ты вырос из Самоса, отправляйся путешествовать - только так ты утолишь жажду познаний. Помни: путешествие и память - суть два средства, возвышающие человека и открывающие ему врата мудрости».
Для жителей Самоса все дороги вели в Милет (греческую колонию). Там юный Пифагор встречается с Фалесом, мудрецом, слава о котором гремела по всей Элладе. Под его руководством Пифагор изучает математику и небесную механику. По совету Фалеса двадцатилетний Пифагор принимает решение отправиться в Египет. Там он прожил 11 лет. Пифагор овладевает премудростями и тайнами египетских жрецов и достигает высших ступеней в храмовой иерархии.
В 526 г. до н. э. в Египет вторглись войска персидского царя Камбиза, и Пифагор вместе с другими жрецами попал в плен. Так он оказался в Вавилоне, где и прожил еще 12 лет.
Долгое пребывание в атмосфере таинства оставило отпечаток в сознании Пифагора. Пора ученичества подошла к концу. Многое было известно, понято, прочувствовано. Ничего нового жрецы уже не могли дать своему талантливому ученику. Возможно, неудовлетворенность бездоказательностью египетской и вавилонской математики ускорила окончательное решение Пифагора возвратиться на родину. Он хотел создать свою школу, в которой ясность логики и твердость доказательств стали бы главным строительным материалом.
Приложение 2
Пифагор - основатель пифагорейской школы
Вернувшись на остров Самос, он так поразил знаниями своих соотечественников, что его считали полубогом. Пифагор собирает вокруг себя юношей из благородных семей и ведет с ними тайные беседы. Поликрат, правитель острова, боясь, что под прикрытием этих бесед против него зреет заговор, приказывает своим людям следить за Пифагором. Возмущенный ученый навсегда покидает родной остров и поселяется в одном из греческих городов южной Италии - Кротоне. Там он сразу привлекает к себе всеобщее внимание и уважение как человек, много странствовавший, многоопытный и дивно одаренный судьбой и природой: с виду он был величав и благороден, а красота и обаяние были у него в голосе. На выступлениях Пифагора собирается до шести сот человек. О силе его воздействия на слушателей говорит такой факт: «Когда он однажды произнес речь, направленную против роскоши, то все женщины отнесли свои нарядные платья в храм Геры, так как ни одна из них не решалась показаться на улице в дорогом одеянии».
С приездом Пифагора в Кротон начинается самый яркий период его биографии. Пифагор основал сообщество своих учеников и последователей - пифагорейскую школу, - которое было одновременно научно-философской школой, религиозно-мистическим союзом, духовным братством.
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства, тайного монашеского ордена, члены которого обязывались вести «пифагорейский образ жизни». Это был одновременно и религиозный союз, и политический клуб, и научное общество. Не только сила личности и мудрость Пифагора, но и высокая нравственность проповедуемых им идей и жизненных принципов притягивала к нему единомышленников. Поначалу именно талант политического оратора и религиозного проповедника, а не мудрость философа и тем более естествоиспытателя, принесли Пифагору успех. Нравственные принципы и правила, проповедуемые Пифагором, и сегодня достойны подражания. Для всех было у него одно правило: беги от всякой хитрости; отсекай огнем, железом и любым оружием от тела болезнь, от души - невежество, от утробы - роскошь, от города - смуту, от семьи - ссору. Есть две поры, учил Пифагор, наиболее подходящие для размышления: когда идешь ко сну и когда пробуждаешься ото сна. День пифагорейцу надлежало закончить стихами: «Не допускай ленивого сна на усталые очи, прежде чем на три вопроса о деле дневном не ответишь: «Что я сделал? Что не сделал? И что мне осталось сделать?» - и начинать день со стихов: «Прежде чем встать от сладостных снов, навеваемых ночью, душой раскинь, какие дела тебе день приготовил».
Эти стихи современны и по прошествии двух с половиной тысячелетий.
Пифагор выработал для себя и своих учеников особый распорядок дня. Встав до восхода солнца, пифагорейцы шли на морской берег встречать рассвет, делали гимнастические упражнения, затем принимали завтрак. В конце дня совершали совместные прогулки, морское купание и ужинали, а после ужина обязательным было возлияние богам и чтение. Как видим, пифагорейцы с равным усердием заботились о физическом и духовном развитии.
Приложение 3
Божественные числа
В основе религиозно-философского учения Пифагора лежало представление о числе как основе всего существующего в мире. «Числа - суть боги на земле», - говорил он. Ритуал посвящения в члены пифагорейского братства был окружен множеством таинств, разглашение которых сурово каралось. Но и попав в орден после строгого отбора и испытательного периода, новички могли только из-за занавеса слушать голос учителя, видеть же его самого разрешалось только после нескольких лет очищения музыкой и аскетической жизнью. Обучение в школе было двухступенчатое, одни ученики назывались «математиками», то есть познавателями, а другие - «акусматиками», то есть слушателями. Математики - те, кто изучал суть науки, акусматики - те, кто прослушивал обобщенный свод знаний.
Акусматики представляли первую ступень в школе Пифагора. Наиболее одаренные акусматики переводились в математики, им разрешалось видеть учителя, вести с ним научные споры. Пифагорейцы узнавали друг друга по звездчатому пятиугольнику - пентаграмме. Они верили, что в числовых закономерностях спрятана тайна мира. Мир чисел жил для пифагорейца особой жизнью, числа имели свой особый жизненный смысл. Числа древними греками мыслились зримо в виде камешков (популярные сегодня слова «калькуляция», «калькулятор» произошли именно от счета камешков, разложенных на песке или на счетной доске - абаке).
Числа-камешки раскладывались в виде правильных геометрических фигур; эти фигуры классифицировались. Так возникли числа, сегодня именуемые фигурными.
1. Линейные числа (то есть простые) - числа, которые делятся на 1 и на себя. Следовательно, их представляли в виде последовательности точек, выстроенных в линию: например, число 5.
2. Плоски^ числа - числа, представляемые в виде произведения двух сомножителей.
3. Треугольные числа (3, 6, 10 и т. д).
Фигурное представление чисел помогало пифагорейцам открывать законы арифметики. Так, представляя плоское число 6 в двух формах, легко «увидеть» переместительный закон умножения.
Одной из главных частей пифагорейской арифметики было учение о четных и нечетных числах. Наряду с математическими истинами в открытиях пифагорейцев было много фантазии и мистики. Так, четные числа они считали несчастными, а нечетные - счастливыми. (Эта традиция сохранилась и поныне в обычае дарить нечетное число цветов)
Важнейшим достижением пифагорейцев было открытие ими совершенных чисел. Натуральное число, равное сумме всех своих делителей:
6 = 1 + 2 + 3;
28 = 1 + 2 + 4 + 7+ 14.
Пифагор по формуле q = 2"(2^(n+1) - 1) смог находить совершенные числа при значениях п, для которых число р = 2^(n+1) - 1 является простым. Первые четыре таких числа были пифагорейцам известны. А есть ли другие совершенные числа? Этот вопрос уже 2500 лет остается открытым.
Приложение 4
Пифагоровы тройки
С теоремой Пифагора связана арифметическая задача: имеются такие тройки натуральных чисел х, у, z, что х^2 + у^2 = z^2. Сегодня эта задача называется задачей Пифагора, а ее решение - тройки натуральных чисел - пифагоровыми тройками. Частные решения были известны в глубокой древности: в Древнем Египте, например, треугольник со сторонами 3, 4, 5 использовали при разметке прямоугольных земельных участков после ежегодного уничтожения их границ разлившимся Нилом. А можно ли найти все решения уравнения x^2+y^2=z^2 в натуральных числах? Занимаясь поисками ответа на данный вопрос, Пифагор нашел формулы, которые в современной символике могут быть записаны так: a = 2n+ 1,b = 2n(n+ 1), с = 2n^2 + 2n+ 1, где n - любое натуральное число.
При различных значениях п можно получить всевозможные наборы пифагоровых троек:
n = 1, (3, 4, 5); n = 2, (5, 12, 13); n = 3, (7, 24, 25).
Треугольник с такими сторонами является прямоугольным. Изучение вавилонских, древнекитайских рукописей показало, что это утверждение было известно задолго до Пифагора. Египтяне и вавилоняне проводили каждое вычисление по рецепту, которому можно было слепо следовать. Эти рецепты неизменно давали правильное решение, и никому и в голову не приходило усомниться в них или подвергнуть анализу логику, лежащую в их основе. Пифагор же хотел понять числа, а не только вслепую пользоваться ими. Его заслуга состояла в том, что он доказал эту теорему. Существует легенда, согласно которой Пифагор принёс в жертву не то одного быка, не то сто быков в честь открытия двух квадратов, сумма которых равна третьему квадрату.
Приложение 5
Иррациональные числа
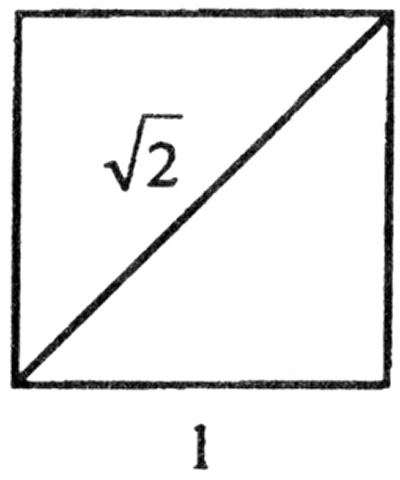
Кроме рациональных чисел, существуют нерациональные. Их называли иррациональными. Это открытие сделали впервые пифагорейцы. Может быть, геометрически, что вероятнее всего, а может быть, алгебраически, основываясь на понятиях «четное», «нечетное». Крупнейший греческий философ Платон писал, что до того, как он узнал о существовании несоизмеримых отрезков, он был подобен неразумному животному.
Открыли, изумились и ... испугались. Это же так противоречило их учению, в основе которого лежали лишь рациональные числа, что они решили засекретить свое открытие.
Будто бы после смерти Пифагора один из его учеников Гиппас, сделав некоторые дополнения к учению Пифагора, поделился ими с другими и рассказал о несоизмеримости диагонали квадрата с его стороной. Тем самым был нарушен обет молчания. Гиппас был изгнан из школы. Позднее, когда он погиб во время кораблекрушения, суеверные пифагорейцы утверждали, что бурю послали боги, чтобы наказать клятвоотступника.
Чтобы уйти от противоречия со своей философией, пифагорейцы пытались допустить существование бесконечно малой общей меры стороны квадрата и его диагонали. Невозможность прийти этим путем к цели привела к тому, что несоизмеримые величины стали восприниматься как «уму непостижимые», как «скандальное исключение».
Между тем теория «несуществующих» чисел сейчас обоснована, и открытые пифагорейцами иррациональные числа понятны и реальны.
Приложение 6
«Теорема невесты»
Данную теорему, носящую в литературе имя Пифагора, в Средневековье в некоторых областях Германии и Франции называли «мостом ослов», а за трудность доказательства, приведенного в книге Евклида «Начала», - «бегством несчастного». У математиков арабского Востока она называлась «теоремой невесты». Дело в том, что в некоторых списках «Начал» Евклида эта теорема называлась «теоремой нимфы» за сходство чертежа с пчелкой, бабочкой, по-гречески - нимфой. Но этим словом греки называли еще некоторых богинь, а также вообще молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово «нимфа» как «невеста», а не «бабочка». Так появилось ласковое название знаменитой теоремы - «теорема невесты».
Сейчас историками математики доказано, что сама теорема Пифагора была известна еще задолго до развития греческой математики, например, в Древнем Египте, Китае.
Приложение 7
Стихи о Пифагоре
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношение
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Рекомендуем посмотреть:
Научно-практическая конференция, посвященная С. В. Ковалевской. Сценарий
Математическая игра для учащихся 7-11 класса
Внеклассное мероприятие по математике 8 класс к неделе математики
Внеклассное мероприятие по математике 7 класс к неделе математики
Внеклассное мероприятие по математике 8-9 классы на неделю математики





