Решение экономических задач на кредиты

Описание материала: Предлагаю вам статью, в которой показаны способы решения экономических задач на кредиты. Описаны два вида кредита: с аннуитетным платежом и дифференцированным платежом. Данный материал будет полезен для учителей математики 10-11 классов при подготовке к ЕГЭ по математике профильного уровня (задача 17). 1. Аннуитетный платеж – представляет собой равные ежемесячные транши (платежи), растянутые на весь срок кредитования. В сумму транша включены: часть ссудной задолженности и начисленный процент. При этом, в первые месяцы (или годы) кредита большую часть транша составляют проценты, а меньшую – погашаемая часть основного долга. Ближе к концу кредитования пропорция меняется: большая часть транша идет на погашение «тела» кредита, меньшая – на проценты. При этом общий размер транша всегда остается одинаковым.
2. Дифференцированный платеж – представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Наибольшие платежи – в первой четверти срока, наименьшие – в четвертой четверти. «Срединные» платежи обычно сравнимы с аннуитетом. Ежемесячно тело кредита уменьшается на равную долю, процент же насчитывается на остаток задолженности. Поэтому сумма транша меняется от выплаты к выплате. Если в задаче присутствуют слова «равными платежами» или «долг уменьшается на одну и ту же величину», то речь идет о дифференцированном платеже. Предлагаю рассмотреть решения экономических задач на кредиты доступными для учащихся способами. Задача 1.
1 января 2015 года Александр Сергеевич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая – 1-го числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?
Решение:
Ответ: 5 месяцев.

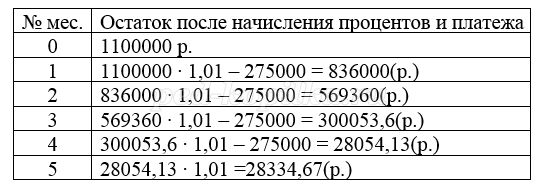
Задача 2.
31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5 годовых. Схема выплаты кредита следующая – 31 декабря следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?
Решение:
Дмитрий взял в банке кредит 4 290 000 рублей.

Дмитрий выплатил кредит за два года, поэтому сумма долга в конце второго года равна 0.
Получим уравнение:
Значит сумма платежа равна 2622050р.
Ответ: 2622050 рублей.
При решении задач на кредиты с дифференцированным платежом начисляемые проценты за весь период кредитования можно вычислить с помощью формулы суммы n-первых членов арифметической прогрессии. И потом найти сумму общего платежа. Считаю, что этот метод будет прост и понятен для учащихся.

Задача 3
15 января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму надо выплатить банку за первые 12 месяцев?
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных «процентов» за 12 месяцев (в млн. р.):

В скобках арифметическая прогрессия. Воспользовались формулой суммы n-первых членов арифметической прогрессии :

За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
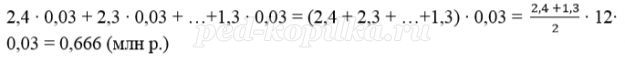
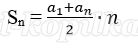
Значит за первые 12 месяцев банку нужно выплатить 1 200 000 + 666 000 = 1 866 000 р.
Ответ: 1 866 000 рублей.

Задача 4
15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Решение:
Пусть в банке взяли кредит S рублей. Платёж за месяц состоит из величины ежемесячного долга (он равен ) и начисленных к остатку процентов. В каждый месяц долг уменьшается на
Сумма начисленных процентов за 5 месяцев:

Всего банку будет выплачено S + 0,03S = 1,03S. Значит общая сумма выплаченных денег от суммы кредита составляет 103%.
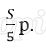
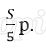
Ответ: 103%.

Задача 5
15 января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку за последние 12 месяцев?
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных процентов за 12 последних месяцев (в млн):

В скобках арифметическая прогрессия. Воспользовались формулой:
За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
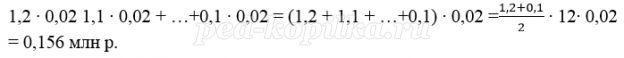
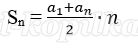
Значит за последние 12 месяцев банку нужно выплатить 1 200 000 + 156 000 = 1 356 000 р.
Ответ: 1 356 000 рублей.

Задача 6
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 99,2 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен и начисленных процентов к остатку. В каждый месяц долг уменьшается на
Значит за 15 месяцев должны заплатить долг – S рублей и ежемесячных процентов, начисленных к остатку:

За 7 месяцев выплачено Из этого условия найдём S.
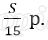
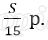
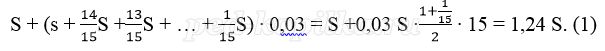
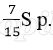
Восьмая выплата состоит из величины ежемесячной выплаты долга и процентов, начисленных на величину долга после седьмой выплаты:

Получим уравнение:
Значит за весь срок кредитования будет выплачено 1 488 000 рублей.
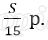
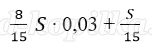
Ответ: 1 488 000 рублей.

Задача 7
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен и начисленных к остатку процентов). В каждый месяц долг уменьшается на
Значит за 9 месяцев должны заплатить долг – S рублей плюс сумму процентов, начисленных к остаткам ежемесячно:

Значит кредит взят под 3% в месяц.
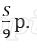
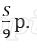
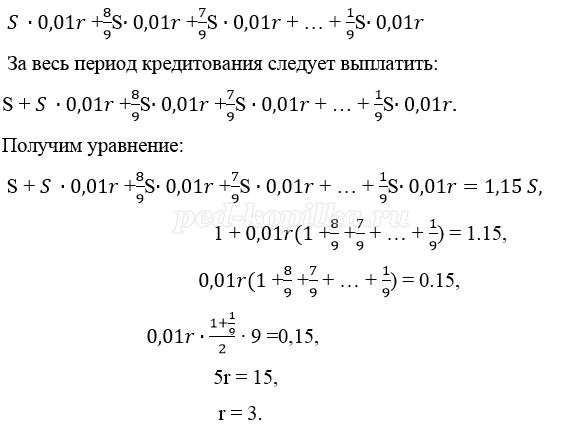
Ответ: 3%.

Задача 8
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен и начисленных к остатку процентов. В каждый месяц долг уменьшается на
Значит за 15 месяцев должны заплатить долг – S рублей и ежемесячных процентов, начисленных к остатку:

За 7 месяцев выплачено Из этого условия найдём S.
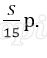
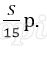
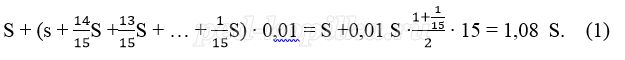
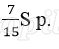
Восьмая выплата состоит из величины ежемесячной выплаты долга и процентов, начисленных на величину долга после седьмой выплаты:

В (1) подставим (2), получим: 1,08 ∙1 500 000 = 1620000
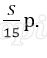
Значит за весь срок кредитования будет выплачено 1 620 000 рублей.
Ответ: 1 620 000 рублей.

Задача 9
15 января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь период кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен и начисленных к остатку процентов. В каждый месяц долг уменьшается на
Значит за 18 месяцев должны заплатить долг – S рублей и сумму ежемесячных процентов, начисленных к остатку:
Значит сумма выплаченных банку денег составляет 119% от суммы долга.
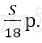
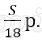
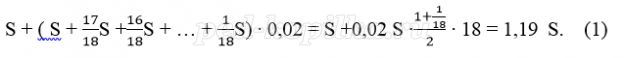
Ответ: 119%.

Задача 10
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за первые 12 месяцев нужно выплатить банку 177,75 тыс. рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен и начисленных к остатку процентов). В каждый месяц долг уменьшается на
За первый год кредитования следует выплатить:

Получим уравнение: 0,5925 S = 177750,
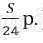
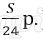
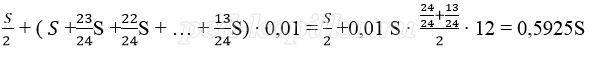
S = 300000
Значит в кредит взяли 300 000 рублей.
Ответ: 300 000 рублей.

Задача 11
15 января планируется взять кредит в банке на 25 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что я сумма денег, которую нужно выплатить банку за весь срок кредитования, на 39% больше, чем сумма, взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен и начисленных к остатку процентов). В каждый месяц долг уменьшается на
Значит за 25 месяцев должны заплатить долг –S рублей плюс сумму процентов, начисленных к остаткам ежемесячно:

Значит кредит взят под 3% в месяц.
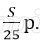
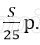
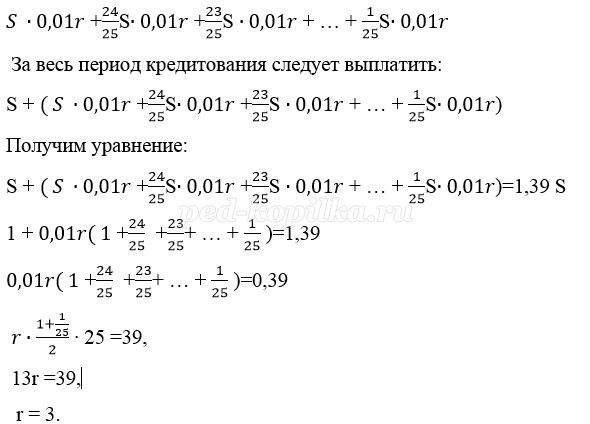
Ответ: 3%.

Задача 12
15 января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за последние 12 месяцев нужно выплатить банку 1597,5 тысяч рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен и начисленных к остатку процентов). В каждый месяц долг уменьшается на
Значит за последние 12 месяцев должны заплатить долг – рублей и ежемесячных процентов, начисленных к остатку:

Получим уравнение: 0,5325 S = 1597500; S = 3 00 000.
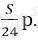
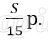
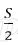
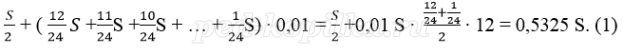
Значит планируется взять 3 000 000 рублей.
Ответ: 3 000 000 рублей.

Литература
И.В.Ященко. Математика. Профильный уровень. Типовые тестовые задания. Издательство «Экзамен», М. 2017.

Рекомендуем посмотреть:

Урок математики в 4 классе Конспект урока математики в 1 классе «Ознакомление с решением составных задач» Конспект урока по математике, 2 класс. Решение задач Конспект урока по химии. Решение расчетных задач, 10 класс

Похожие статьи:

Контрольная работа с дескрипторами для 2 класса по теме «Решение задач» по системе Л.В. Занкова