Урок геометрии, 8 класс. Теорема Пифагора. Конспект с презентацией

Описание материала: предлагаю Вам конспект урока геометрии на тему: «Теорема Пифагора». Данный материал будет полезен учителям, работающим в 8-ых классах. Это урок формирования новых знаний и умений учащихся. Урок проводится с использованием презентации. Все задания, рисунки воспроизводятся через мультимедийный проектор на экране.
Цель урока: изучить теорему Пифагора и рассмотреть способы решения задач, рассмотреть вариант доказательства.

Задачи:
Образовательная:
- исследовать закономерности между сторонами прямоугольного треугольника;
- изучить теорему Пифагора;
- формировать умения применять теорему Пифагора при решении задач;
Развивающая: способствовать развитию внимания, мышления, расширения кругозора;
Воспитательная: способствовать формированию потребности в знаниях, интереса к математике, целеустремленности в достижении поставленной цели.
Тип урока: формирование новых знаний и умений.
Оборудование: экран, проектор, компьютер, карточки с заданиями, смайлики из картона.
Ход урока
1. Организационный момент.
Проверка настроения: приём “Мордашки” (у каждого ученика на столе 3 смайлики, нужно показать ту, которая соответствует настроению).

2. Актуализация опорных знаний.
1. Работа в парах, выполнение теста с взаимопроверкой в тетрадях, анализ результатов тестирования
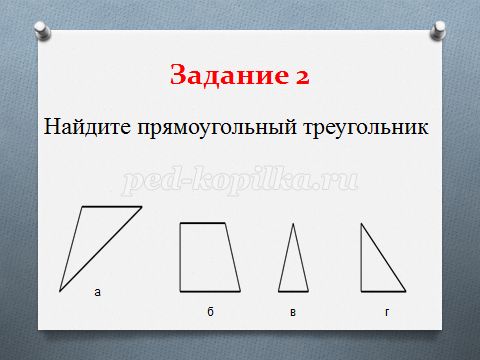
1) Треугольник называется прямоугольным, если у него один из углов: (слайд 2)

2) Найдите прямоугольный треугольник: (слайд 3)

3) Назовите прилежащий катет угла М в треугольнике КМР (слайд 4)

) Какие из треугольников являются прямоугольными? (слайд 5)

(слайд 6)
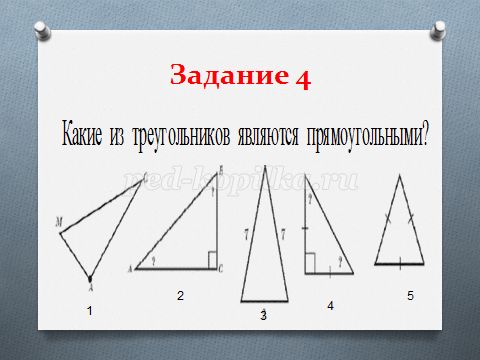
5) Чем является сторона АВ в треугольнике №2?
6) Какая сторона прямоугольного треугольника называется гипотенузой?
7) Чем являются стороны АС и ВС в треугольнике №2?
8) Какие стороны прямоугольного треугольника называются катетами?

(учащиеся обмениваются записями и выполняют проверку).

3. Подготовительный этап
Учитель предлагает ученикам провести построения в тетради:
1. Начертите прямоугольный треугольник АВС с прямым углом С.
2. Измерьте длины его сторон
3. Вычислите, чему равен квадрат гипотенузы.
4. Вычислите квадраты катетов.
5. Найдите сумму квадратов катетов.
6. Сравните квадрат гипотенузы и сумму квадратов катетов.
7. Какой можно сделать вывод?
(Ученики отвечают) Квадрат гипотенузы равен сумме квадратов катетов.

Учитель: мы с вами опытным путём доказали теорему, которая является одной из важнейших теорем геометрии, теорему Пифагора, которую он доказал в 6 в. до н.э.. Однако она была известна еще в вавилонских текстах за 1200 лет до Пифагора.
Сегодня теорема Пифагора насчитывает около 500 возможных, включая глупые доказательства.
Так доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Ponsasinorum – ослиный мост или elefuga – бегство убогих, так как некоторые ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания и прозванные поэтому “ослами” не были в состоянии преодолеть теорему Пифагора, служившую для них вроде непроходимого моста.
Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же “ветряной мельницей”, составляли стихи вроде “Пифагоровы штаны на все стороны равны”, рисовали карикатуры.

4. Изучение новой темы.
Учитель: Итак, тема нашего урока: «Теорема Пифагора» (слайд 7)

(запись в тетрадь).
Откройте учебники на с.130 и прочитайте теорему Пифагора, сформулируйте её.
(Учащиеся отвечают)
Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Условие: в прямоугольном треугольнике. Заключение: квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора позволяет установить следующие соотношения, применяемые при решении задач: а2=с2–b2; а2=с2-b2
b2 = с2 – а2;

Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путём
К результату мы придём.

Учитель: Ребята, а вы знаете, какие треугольники называют пифагоровыми? (отвечают) (слайд 9)
Это треугольники, у которых длины сторон выражаются целыми числами. А треугольник, у которого катеты равны 3 и 4 единицы, а гипотенуза 5 единиц, называют египетским, так как он был известен еще древним египтянам.

5. Закрепление знаний.
Применение теоремы Пифагора для решения практических задач:
Каждой группе (можно условно разделить по рядам) предлагается решить задачу по готовому чертежу. На выполнение одного задания 3-4 мин.
1) Вычислите, если возможно: (учащиеся решают, затем один из группы озвучивает решение классу) (слайд 10)
1. Сторону АС треугольника АВС (рис. 1); - 1 группа
2. Сторону MN треугольника KMN(рис. 2); - 2 группа
3. Сторону KP треугольника KPR(рис.3); - 3 группа

Ответы: 4)корень из 5 5) 5; 6) в) строну треугольника вычислить нельзя т.к. не известен вид треугольника.
2) Решите задачу по данному чертежу:
1 группа: (слайд 11)

2 группа: (слайд 12)

3 группа: (слайд 13)

Один конец каждого троса должен крепиться на высоте 12 м., другой на земле на расстоянии 5 м. от мачты. Хватит ли 50 м. троса для крепления мачты?

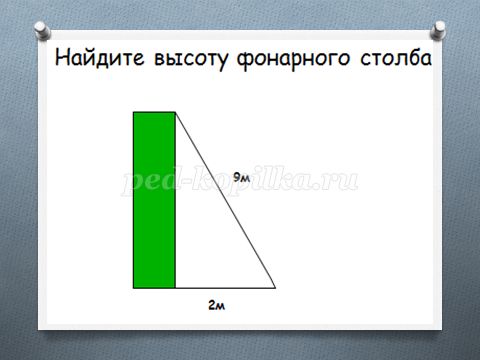
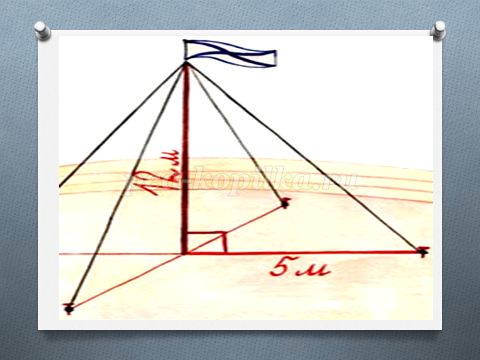
Ответы: 1)корень из 13 2)корень из 77 3) 13, да
3) Решить задачу №483 (а, б, в) по группам.
6. Составление кластера «Теорема Пифагора» (слайд 14)

Учащиеся фиксируют в тетрадь.

7. Рефлексивно-оценочный этап
Домашнее задание: п.54 (слайд 15)

Решить задачу (задачи распечатаны на карточках)
1 уровень. Необходимо обнести забором участок имеющий форму прямоугольного треугольника с катетами 8см и 15см. Как найти длину этой изгороди?

2 уровень. На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой -20 локтей. Расстояние между их основаниями - 50 локтей.
На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно.
На каком расстоянии от основания более высокой пальмы появилась рыба?

3 уровень. Изучи другие способы доказательства т. Пифагора.

Рефлексия. Организация рефлексии на основе метода неоконченных предложений.
Ответь на 3 любых предложений (учащиеся отвечают) (слайд 16)

Я почувствовал, что…
Было интересно…
Меня удивило…
Своей работой сегодня я…, потому что...
Мне захотелось…
Мне больше всего удалось…
Заставил задуматься…
Навел на размышления…
Сегодня я узнал…
Было трудно…, потому что...
Я выполнял задания…
Я понял, что…
Теперь я могу…, потому что...
Я приобрёл…
Я научился…
Задания для меня показались…, потому что...
Для меня было открытием то, что…
Мне показалось важным…, потому что...

Выставление оценок.
Учитель благодарит ребят за работу.

Литература:
«Геометрия 7-9 классы» учебник для 7-9 классов (авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др.,– М: «Просвещение», 2017)
Спасибо за внимание!

Скачать эту работу

Скачать эту презентацию

Рекомендуем посмотреть:

Конспект урока геометрии "Теорема Пифагора", 8 класс Конспект урока по геометрии в 8 классе с презентацией. Площади четырёхугольников Конспект урока геометрии "Красота симметрии" для 8 класса с презентацией Технологическая карта урока геометрии в 8 классе по теме: Теорема Пифагора

Похожие статьи:

Биография Пифагора кратко для детей начальной школы