Конспект урока геометрии "Теорема Пифагора", 8 класс

Учитель математики Зайцева Татьяна Евгеньевна.
Место работы МБОУ СОШ № 13, г.Новосибирск.
Аннотация: разработка урока по геометрии в 8 классе на тему "Теорема Пифагора". Закрепления учебного материала, применение теоремы Пифагора в решении практических задач.Цель:
1. Закрепить умение применять теорему Пифагора и теорему, обратную теореме Пифагора, при решении прикладных задач.
2. Развить самостоятельность и познавательный интерес в изучении геометрии, логическое мышление и навыки самоконтроля.
3. Воспитать культуру математической речи, уважительное отношение к мнению окружающих.
Задачи:
1) Помогать учащимся в формировании умений и навыков работы с дополнительной информацией, умений обобщать и самостоятельно делать выводы.
2) Продолжить формировать навыки анализа, умения строить доказательства при изучении теоремы.
3) Помогать учащимся в нахождении значений применяемости теоремы для человечества в быту, строительстве в разные эпохи существования человечества.
4) Воспитывать эстетический вкус у учащихся через восприятие картин и красоты;
5) Помогать в развитии у учащихся познавательного интереса к изучению геометрии;
5) Продолжить формирование умений представлять результаты своей работы.
Тип урока: урок закрепления полученных знаний
Формы работы: фронтальная, групповая, индивидуальная, самостоятельная
Оборудование:
• персональный компьютер
• мультимедийный проектор
• экран
• авторская презентация, подготовленная с помощью Microsoft Power Point
• CD – диск, мультимедийный курс «ПЛАНИМЕТРИЯ», серия «Открытая математика» ФИЗИКОН (www.physicon.ru), полный интерактивный курс математики для общеобразовательных учреждений России, ВЕРСИЯ 2.5
• карточки с заданиями

Структура урока
1. Организационный момент
2. Актуализация имеющихся знаний обучающихся по теме (формулировка и доказательство теоремы Пифагора, решение задач по готовым чертежам)
3. Сообщения обучающихся (историческая справка, рассмотрение классических доказательств теоремы Пифагора)
4. Решение практических и древних задач
5. Проверочная работа с самоконтролем
6. Итог урока. Рефлексия
7. Домашнее задание

ХОД УРОКА:
1. Организационный момент урока: приветствие, проверка готовности к уроку (рабочих тетрадей, учебников, письменных принадлежностей).
Тема урока слайд 1, цель урок слайд 2, план урока слайд 3 . (1-2 минуты)
2. Актуализация знаний, полученных учащимися на предыдущем уроке (5 минут):
• Формулировка теоремы Пифагора; слайд 4
• Формулировка теоремы, обратной теореме Пифагора слайд 5
Доказательство теоремы Пифагора можно осуществить с помощью мультимедийного диска «ПЛАНИМЕТРИЯ», версия 2.5, серия «ОТКРЫТАЯ МАТЕМАТИКА» Физикон.
(Модели. 5.2. Доказательство теоремы Пифагора)


Данная модель иллюстрирует геометрическое доказательство теоремы Пифагора.
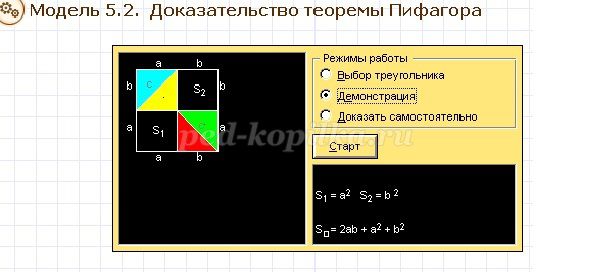
С помощью мыши можно выбрать произвольный прямоугольный треугольник.
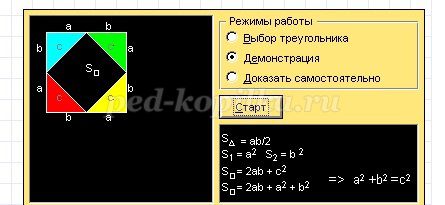
В режиме «Демонстрация» модель автоматически показывает геометрическое доказательство теоремы Пифагора.
В режиме «Доказать самостоятельно» Вы можете сделать необходимые для доказательства самостоятельные построения, меняя положения треугольников в квадрате.
С целью актуализации знаний обучающимся предлагаются задачи по готовым чертежам.
2.1. Слайд 6. Найти неизвестную сторону треугольника.

2.2. Слайд 7. Решите задачу (нахождение периметра ромба с использованием теоремы Пифагора)

2.3. Слайд 8. Задача на применение теоремы, обратной теореме Пифагора


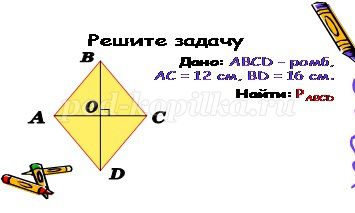
3. Сообщения учащихся (5-7 минут).
3.1. Экскурс в историю. Знакомство с жизнью и достижениями великого ученого. История открытия теоремы Пифагора.
3.2. Обучающимся предлагается сравнить предложенное доказательство с доказательством, рассмотренным на предыдущем уроке, выявить сходства и различия.

4. Закрепление теоремы Пифагора при решении практических и древних задач (10-15 минут). Работа в парах с последующей проверкой.
4.1. Задача №1 (слайд 9) «Древнерусская задача». Условие задачи разбирается устно, чертеж и решение учащиеся записывают в тетрадях. (Ответ: 44 стопы).

4.2. Задача №2 (слайд 10) «Тополь у реки» - для устного решения. (Ответ: 8 футов). [/i]

4.3. Задача №3 (слайд 11). Нахождение длины главной аллеи Центрального парка города Новосибирска. Условие задачи разбирается устно, чертеж и решение учащиеся записывают в тетрадях, 1 ученик работает у доски. (Ответ: 412 м).

4.4. Задача № 4 (мультимедийный CD – диск, ПЛАНИМЕТРИЯ)
Содержание. ГЛАВА 5. Решение треугольников.5.1. Прямоугольный треугольник. Задачи. Задача № 6.


5. Самостоятельная работа с самоконтролем (15 минут).
Учащимся предлагается ТЕСТ, карточки (см. приложение) с заданиями на 2 варианта. Фамилию и ответы учащиеся записывают на карточках, а краткое решение в тетрадях.


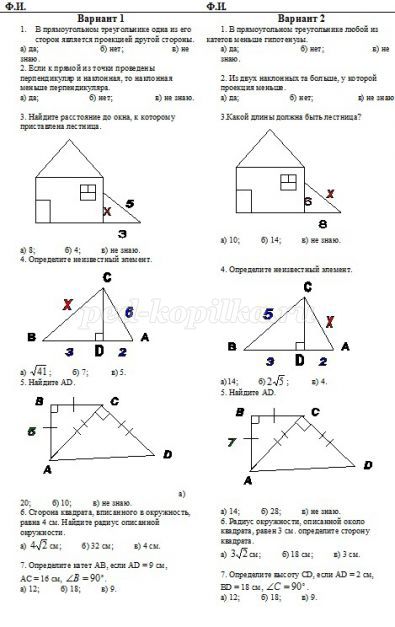
6. Итог урока. Рефлексия (3-5 минут). (слайд 12)
В конце урока подводится его итог, обсуждение того, что узнали, и того, как работали – т.е. каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы класса, увлекательность и полезность выбранных форм работы.
Ребята высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…

7. Домашнее задание.
1. Фронтон Большого театра в Москве имеет форму равнобедренного треугольника с боковыми сторонами по 21,5 м и основанием 42 м (размеры приближены). Вычислите площадь фронтона.
2. Найдите ещё одно доказательство теоремы Пифагора (по выбору).

Рекомендуем посмотреть:

Кроссворд по геометрии с ответами для 8 класса Конспект урока алгебры по теме "Квадратные уравнения" с использованием интерактивного учебного пособ Внеклассное мероприятие по математике, 7-9 класс Технологическая карта урока геометрии в 8 классе по теме: Теорема Пифагора

Похожие статьи:

Биография Пифагора кратко для детей начальной школы

Программа факультатива по математике, 8-9 класс

Олимпиада по математике в 8 классе с решением

Конспект урока по алгебре в 8 классе. Решение квадратных уравнений

Открытый урок по алгебре в 8 классе «Решение квадратных уравнений по формуле»