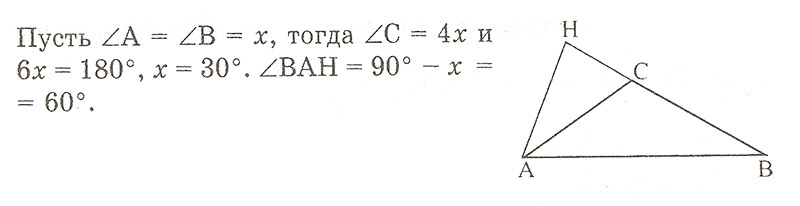Олимпиада по математике в 8 классе с решением

Математическая олимпиада в 8-м классе.

1. Найдите трехзначное число, если оно равно кубу своей последней цифры и квадрату числа, составленного из двух его первых цифр. (Ответ: 729)

Решение.

Примечание: Задачу можно решить простым перебором, так как трехзначных кубов всего 5.

2. Найдите несократимую дробь, которая не меняет своей величины от прибавления к числителю 14, а к знаменателю 21. (Ответ: 2/3).

Решение.

3. В треугольнике ABC углы А и В равны, а угол С вдвое больше их суммы. Чему равен угол между стороной АВ и высотой, опущенной из вершины А на ВС? (Ответ: 60°)

Решение. Угол С — тупой, так как его величина больше половины суммы углов треугольника, т.е. больше 90°. Поэтому высота АН опущена на продолжение стороны ВС.

4. Какое максимальное число королей, не бьющих друг друга, можно расставить на шахматной доске 8Ч8? (Ответ: 16)

Решение. В квадрате 2x2 можно поставить не более одного короля. Непересекающихся квадратов 2x2 на шахматной доске 16, следовательно, можно поставить не более 16 королей. Действительно, можно поставить 16 королей, если ставить их, например, в левый верхний угол каждого квадрата.

5. Мышка грызет куб сыра с ребром 3, разбитый на 27 единичных кубиков. Когда мышка съедает какой-нибудь кубик, она переходит к другому кубику, имеющему общую грань с предыдущим. Может ли мышка съесть весь куб, кроме центрального кубика?

Решение. 26 единичных кубиков, отличных от центрального, будем считать белыми или черными в шахматном порядке: 12 кубиков, имеющих ровно по 2 грани на поверхности большого куба, назовем белыми, остальные 14 — черными. При такой раскраске два соседних кубика, имеющих общую грань, имеют разный цвет. Чтобы мышка смогла съесть указанные 26 кубиков, их нужно разбить на 13 пар, в каждой паре по одному белому и черному. Но это невозможно.

Рекомендуем посмотреть:

Программа факультатива по математике, 8-9 класс

Олимпиада по математике в 7 классе с решением

Олимпиады по математике, 2-4 класс