Олимпиадные задания по математике 7-8 класс с решениями и ответами

Математические олимпиадные задачи (7-8 классы) с ответами

Задача 1.

Колумб открыл Америку в XV веке. В каком году совершено это открытие, если известно следующее:

а) сумма цифр, обозначающих этот год, равна 16;

б) при делении цифры десятков на цифру единиц в частном получится 4, а в остатке 1.

Задача 2.

Пете дали стакан чёрного кофе. Он отпил часть стакана 1/5 часть и долил молоком, потом еще раз отпил 1/5 стакана и долил молоком. Выпив затем 3/5 стакана, он подсчитал, что в оставшейся части кофе только на 28 см3 больше, чем молока. Найти объём стакана.

Задача 3.

Окрашенный куб с ребром 10 см распилили на кубики с ребром в 1 см. Сколько из них окажется с одной, двумя и тремя окрашенными гранями?

Задание 4.

Если между цифрами двузначного числа вписать нуль, то полученное трёхзначное число будет в 9 раз больше первоначального. Найти двузначное число.

Задание 5.

Найти сумму:

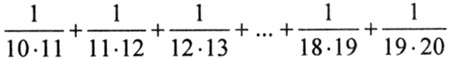
Задача 6.

Товарный поезд имеет в длину 1 км и движется со скоростью 50 км/ч. За какое время он пройдёт тоннель длиной в 1 км?

Задача 7.

Поезд проходит мост длиной 450 м за 45 с, а мимо будки стрелочника он проходит за 15 сек. Вычислить длину поезда и его скорость.

Задача 8.

Электропоезд длиной 18 м проехал мимо километрового столба за 9 с. Сколько времени понадобится ему, чтобы проехать мост длиной 36 м?

Задание 9.

Вычислить наиболее рациональным способом:

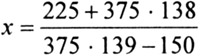
Задание 10.

Найти 12 таких последовательных целых чисел, что сумма десяти первых из них равна сумме двух последующих.

Задание 11.

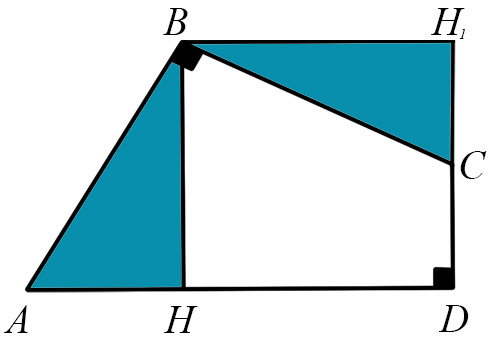
В четырёхугольнике ABCD углы В и D - прямые, а стороны АВ и ВС равны. Определить его площадь, если известно, что его высота равна ВН = 1.

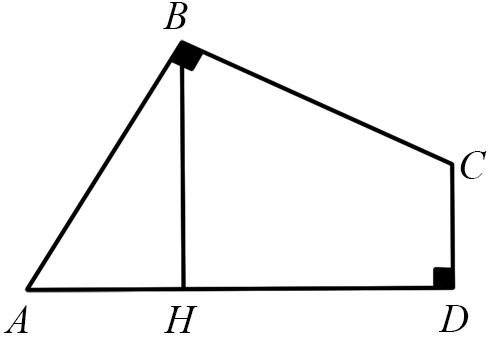
Задача 12.

Вдоль беговой дорожки на равных расстояниях друг от друга стоят 12 флажков. Первый флажок стоит у старта. У 8-го флажка спортсмен был через 8 с. Через сколько секунд он будет у 12-го флажка при постоянной скорости?

Задачи к олимпиаде в 8 классе

Задача 13.

На некотором острове живут 2 племени: рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник, попавший на остров, нанял себе слугу. Однажды, гуляя по острову, путешественник увидел местного жителя и послал слугу узнать, кто это. Вернувшийся слуга ответил, что, по словам встреченного, он - из племени рыцарей. Из какого племени слуга путешественника?

Задача 14.

Имеется три груды камней: в первой - 1996 штук, во второй - 996, в третьей - 96 камней. Одним ходом разрешается либо убрать из каждой груды по одному камню, либо половину камней из какой-либо груды (если в ней чётное число камней) переложить в любую другую. Можно ли добиться того, чтобы во всех трёх грудах не осталось ни одного камня?

Задачи к олимпиаде в 7 классе

Задача 15.

Из двух городов вышли одновременно навстречу друг другу 2 автомобиля. Первый за 2,4 часа проехал 9/10 всего расстояния между городами, а второй за 2 часа проехал 13/140 этого расстояния. С какой скоростью ехал каждый автомобиль, если до места встречи второй проехал 351 км?

Задача 16.

Если основание треугольника ABC разделить на 3 части и точки деления соединить с вершиной треугольника, то получится 6 треугольников: ABD, BDE, ВЕС, АВЕ, DBC и АВС. Сколько треугольников получится, если основание АС разделить на n частей? Ответ обоснуйте.

Задача 17.

В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что 2 города соединены авиалинией в том и только в том случае, если двузначное число, составленное из цифр - названий этих городов, делится на 3. Можно ли добраться из города 1 в город 9? Ответ объясните.

Задание 18.

Произведение четырёх последовательных натуральных чисел равно 3024. Найдите эти числа. Ответ объясните.

Задание 19.

Дан угол в 36°. Как с помощью циркуля и линейки построить угол в 99°? Запишите план построения.

Задача 20.

В футбольном турнире, в котором каждая из 8 участвующих команд сыграла с каждой командой по одному разу, команды набрали следующее число очков: 14, 12, 8, 8, 6, 4, 3, 1. Сколько очков команды, занявшие первые 4 места, потеряли в играх с остальными командами (за выигранную игру команда получает 2 очка, за ничью - 1 очко, за проигрыш - 0 очков)? Ответ объясните.

Примечание. Рассуждения при решении задач, которые решаются логически, должны быть краткими, но полными.

Задача 21.

Я еду в поезде, который идёт со скоростью 40 км/ч, и вижу, как в течение 12 секунд мимо моего окна в противоположном направлении проходит скорый поезд, имеющий длину 300 м. С какой скоростью шёл встречный поезд?

Задача 22.

В тёмной кладовой лежат ботинки одного размера: 10 пар чёрных и 10 пар коричневых. Найдите наименьшее число ботинок, которое нужно взять из кладовой, чтобы среди них оказалась хотя бы одна пара одного цвета (считать, что в темноте нельзя отличить не только цвет ботинка, но и левый от правого).

Задача 23.

Морская вода содержит 5 % соли. Сколько килограммов пресной воды нужно прибавить к 40 кг морской воды, чтобы содержание соли в смеси составляло 2 %?

Задание 24.

Часы показывают час дня. Найти ближайший момент времени, когда часовая и минутная стрелки совпадут.

Задание 25.

Восстановите цифры и знаки действий.

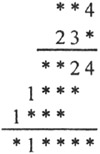
Задача 26.

Цены снижены на 20 %. На сколько процентов больше можно купить товаров на ту же зарплату?

Задача 27.

Можно ли разлить 50 литров бензина по трём бакам так, чтобы в первом баке было на 10 литров больше, чем во втором, а после переливания 26 литров из первого бака в третий в третьем баке стало столько же, сколько во втором?

Задача 28.

В одной из вершин: а) октаэдра; б) куба - сидит муха. Может ли она проползти по всем рёбрам ровно по одному разу и возвратиться в исходную вершину? (Октаэдр представляет собой две четырёхугольные пирамиды, склеенные по основаниям.)

Задание 29.

Дано 6 натуральных чисел. Все они различны и дают в сумме 22. Найти эти числа и доказать, что других нет.

Задача 30.

На доске написаны числа 0, 1,0, 0. За один шаг разрешается прибавлять единицу к любым двум из них. Можно ли, повторяя эту операцию, добиться, чтобы все числа стали равными?

Задание 31.

Внутри квадрата ABCD расположен квадрат KMXY. Доказать, что середины отрезков АК, ВМ, СХ и DY также являются вершинами квадрата.

Задание 32.

Имеются 552 гири массой 1, 2, 3, 552 г. Разложите их на 3 равные части по массе.

Задание 33.

Возьмите 18 спичек. Расположите их на столе и проведите игру. Каждый из двух играющих по очереди берёт спички. За один ход можно брать 1, 2, 3 или 4 спички. Выигрывает тот, кто берёт последнюю спичку. Рассчитайте, сколько спичек должен брать начинающий игру, чтобы всегда выигрывать.

Задание 34.

Найти признак делимости на 7 числа вида 100...01.

Задача 35.

Аня живёт на 19-м, а Саша - на 96-м этаже 100-этажного дома. Лифт в доме имеет только 2 кнопки: «+7» (поднимает на 7 этажей) и «-9» (опускает на 9 этажей). Смогут ли Аня с Сашей ездить друг к другу в гости на лифте?

Задача 36.

В компании из 7 детей для каждого мальчика найдутся не менее трёх других мальчиков, которые родились в одном месяце. Докажите, что все 7 мальчиков родились в одном месяце.

Задание 37.

Нарисуйте 8 точек и соедините их отрезками так, чтобы отрезки не пересекались, а через каждую точку проходило ровно 4 отрезка.

Задание 38.

В трёх различных положениях кубик выглядит так, как показано на рисунке 3. Определить окраску граней кубика (следует указать, как раскрасить каждую грань или нарисовать развёртку).

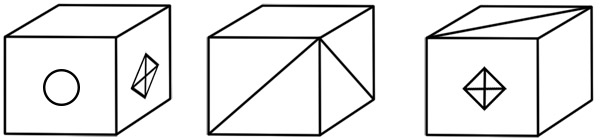
Задача 39.

Аквариум имеет форму прямоугольного параллелепипеда. Если смотреть на аквариум спереди, то рыбка проплыла, как показано на рисунке (а), а если смотреть справа, то как на рисунке (б). Как выглядел маршрут рыбки, если смотреть на аквариум сверху?

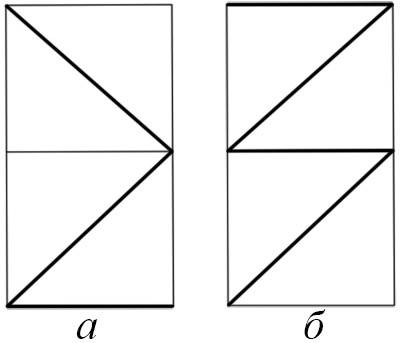
Задание 40.

Можно ли оклеить куб прямоугольниками так, чтобы каждый из них граничил (по отрезку) ровно с пятью другими прямоугольниками?

Задача 41.

Пять студентов стали победителями конкурса, набрав по 22, 21 и 20 баллов, заняв соответственно первые, вторые и третьи места. Сколько студентов завоевали каждое призовое место, если вместе они набрали 104 балла?

Задача 42.

На доске написаны в строку 2005 целых чисел. Доказать, что одно из них можно стереть, и сумма оставшихся чисел будет чётной. Верно ли это утверждение для 2006 чисел?

Задача 43.

Каждый служащий агентства владеет хотя бы одним иностранным языком: английским, французским или немецким. Согласно статистике, 37 % служащих владеют двумя из этих языков, 15 % - немецким и английским одновременно, 4 % - всеми тремя языками, а 56 % не знают французского языка. Сколько процентов служащих знают только французский язык?

Задание 44.

Вычислить:

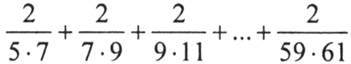
Задание 45.

Найти сумму:

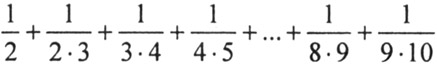
Задание 46.

Вычислить:

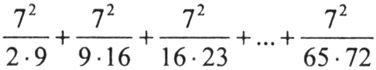
Задание 47.

Дана доска в 19 х 19 клеток. На каждой клетке поставлено по шашке. Можно ли переставить шашки так, чтобы каждая шашка оказалась на соседней клетке (по горизонтали или по вертикали, но не по диагонали)?

Задача 48.

В корзине лежат рыжики и грузди, всего 30 грибов. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов - хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине?

Задание 49.

Придумайте раскраску граней кубика, чтобы в трёх различных положениях он выглядел так, как показано на рисунке. Укажите, как раскрасить невидимые грани, или нарисуйте развёртку.

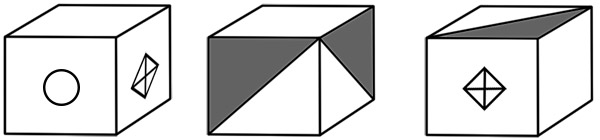
Задача 50.

В Мексике экологи добились закона, по которому каждый автомобиль хотя бы один день в неделю не должен ездить (владелец сообщает полиции номер автомобиля и «выходной» день недели этого автомобиля). В некоторой семье все взрослые желают ездить ежедневно (каждый по своим делам!) Сколько автомобилей должно быть в семье, если в ней: а) 5 человек? б) 8 человек?

Задача 51.

В парке гуляли люди со своими собаками и кошками. Собак было больше, чем людей. У собак и людей вместе было 100 голов и ног. А собак и людей вместе было втрое больше, чем кошек. Сколько кошек было в парке?

Задача 52.

Хулиганы Петя и Вася порвали стенгазету. Петя рвал каждый кусок на 7 частей, а Вася - на 13. Собрали 2001 кусок стенгазеты. Учитель утверждает, что собрали не всё. Прав ли он?

Задача 53.

4 мальчика - Андрей, Витя, Саша и Дима - выбирают по одному мячу чёрного, синего, красного и белого цвета. Требуется узнать, какого цвета оказались у них мячи, если в каждом из следующих утверждений по крайней мере одна часть верна:

а) Андрей взял чёрный мяч, Витя - синий;

б) Дима взял красный мяч, Витя - чёрный;

в) Витя взял белый мяч, Дима - синий.

Задание 54.

В вершинах куба записаны числа: 1, 2, 3, 4, 5, 6, 7, 8. На гранях куба записаны суммы чисел, стоящих в вершинах куба. Могут ли такие суммы выражаться шестью последовательными числами?

Задание 55.

В походе 5 ребят делили три одинаковых булки. Ребята хотели разделить булки поровну, но один из них, не подумав, разрезал одну булку пополам, а другую - на три равные части. Как теперь надо разрезать целую булку, чтобы исправить ситуацию, то есть дать всем поровну?

Задача 56.

Кузнец бьёт молотом по наковальне 4 раза в течение 12 с. Сколько ему потребуется времени, чтобы нанести по наковальне 8 ударов?

Ответы

Задача 1.

Пусть год десятков обозначим через х, число единиц - у; XV век составит: 1000 + 400 + 10х + у. Сумма цифр равна: 1 + 4 + х +у = 16. Частное и остаток: х:у = 4(1), или 4у + 1 = х. Составим систему:

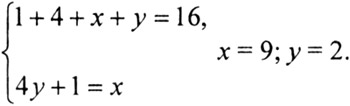
Ответ: 1492 год.

Задача 2.

Пусть х см3 - объём стакана. Выразим объём кофе и молока в стакане:

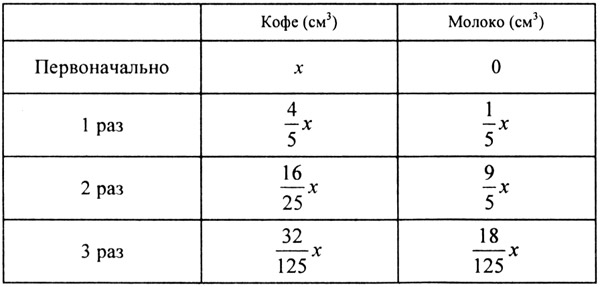
Получаем уравнение:

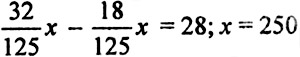
Ответ: 250 см³ - объём стакана.

Задача 3.

С тремя гранями - 8 кубиков (вершины куба); с 2-х сторон: (10 - 2) · 8 = 64 (кубика); с одной стороны: (10 - 2) · (10 - 2) · 6 = 384 (кубика). Итого: 8 + 64 + 384 = 456 (кубиков).

Задание 4.

Число 45.

Задание 5.

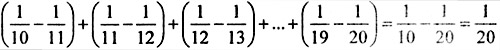
Задача 6.

1 + 1=2 (км) - длина поезда и тоннеля; 2 : 50 = 0,04 ч = 2,4 мин.

Задача 7.

45 - 15 = 30 (с) - время, за которое проходит мост любая точка поезда; 450 : 30 = 15 (м/с) - скорость поезда; 15 · 15 = 225 (м) - длина поезда.

Ответ: 225 метров.

Задача 8.

18:9 = 2 (м/с) - скорость поезда; 18 + 36 = 54 (м) - должен проехать поезд; 54 : 2 = 27 (с) понадобится поезду.

Ответ: 27 секунд.

Задание 9.

Задание 10.

х + (х + 1) + (х + 2) + (х + 3) + (х + 4) + (х + 5) + (х + 6) + (х + 7) + (х + 8) + (х + 10) = (х + 10) + (х + 11).

х = - 3.

Ответ: -3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7; 8.

Задание 11.

Если повернуть треугольник АВН вокруг точки В на 90°, то четырёхугольник DHBH1 окажется квадратом. Следовательно, он, как и четырёхугольник ABCD, имеет площадь, равную 1.

Задача 12.

От первого до 8 флажка 7 промежутков, значит, промежуток спортсмен пробегает за 8/7 секунды, а 11 промежутков (от 1-го до 12-го флажка) - за 11 · (8/7) = (88/7) = 12 (4/7) с.

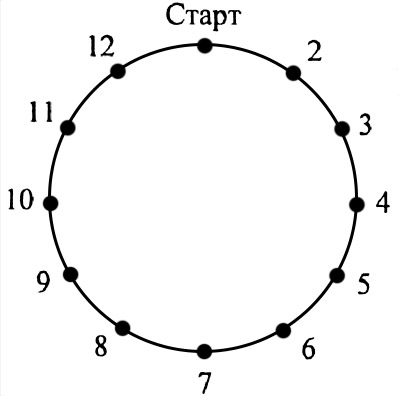
Ответ: через 12(4/7) секунды.

Задача 13.

Если встреченный абориген - рыцарь, то он скажет слуге правду, то есть что он рыцарь. Если встреченный абориген - лжец, то он солжёт и скажет слуге, что он - рыцарь. Следовательно, слуга сказал путешественнику правду, значит, слуга - рыцарь. Ответ: слуга - рыцарь.

Задача 14.

После каждого хода остаток от деления на 3 общего количества камней не меняется. Общее количество камней вначале было: 1996 + 996 + 96 = 3088 = 3 · 1029 + 1 (штук). Это число не делится на 3, следовательно, нельзя добиться, чтобы во всех грудах не осталось камней.

Указания по проверке. За один ответ без обоснований - 0 баллов. Если отмечено, что при любом ходе остаток от деления общего числа камней на 3 не меняется - более 4 баллов.

Задача 15.

Пусть 1 - расстояние между городами.

Ответ: скорость первого автомобиля - 40,5 км/ч, скорость второго-35,1 км/ч.

Задача 16.

Пусть основание разделено на п частей. Тогда из вершины В выходит n + 1 отрезков; пронумеруем их от 1 до n + 1 (ВА1 - первый (1), ВА2 — второй (2), ..., ВАn+1 – (n + 1)- й).

Первый выходящий из вершины В отрезок с каждым из n последующих определяет треугольник, общее число этих треугольников равно n.

Второй отрезок - с n - 1 последующими (треугольник, определяемый с первым отрезком, уже подсчитан), третий определяет n - 2 треугольника, n-й отрезок с (n + 1)-м определяет один треугольник.

Поэтому общее число образовавшихся треугольников равно: n + (n -1) + (n - 2) +... + 2 +1 = (n -1) + ((n -1) + 2) + ((n - 2) + 3) +... = (n + 1) · (n/2)

Задача 17.

Составим граф. Из графа видно, что ответ на поставленный вопрос отрицательный.

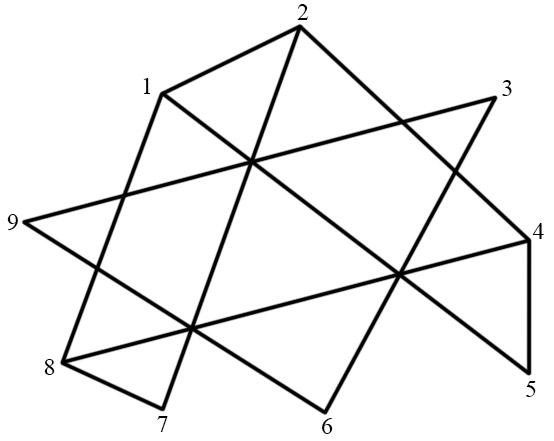
Ответ: нельзя.

Задание 18.

Все числа не могут быть больше 10 (3024 < 10000). Среди этих чисел нет 5 и 10. Поэтому искомыми числами могут быть 1, 2, 3, 4 или 6, 7, 8, 9. Условию удовлетворяют 6, 7, 8, 9.

Задание 19.

Данный угол разделим с помощью циркуля и линейки на 4 равные части по 9°. Затем построим угол в 90° и к нему пристроим с помощью циркуля и линейки угол в 9°.

Задача 20.

Первые четыре команды сыграли с остальными 4 · 4 = 16 (матчей), а между собой (4 · 3)/2 = 6 (матчей), и поэтому наибольшее число очков, которое они могли набрать вместе, равно: 22 · 2 = 44 (очка). В действительности они набрали 42 очка и, следовательно, в играх с остальными командами они потеряли 2 очка.

Ответ: потеряли 2 очка, набрали 42 очка.

Задача 21.

Скорость встречного поезда относительно моего: 300 : 12 (м/с) = 25 (м/с) = 25 · 3600 : 1000 км/ч = 90 км/ч. Скорость второго поезда: 90 - 40 = 50 (км/ч).

Ответ: 50 км/ч.

Задача 22.

Если взять 20 или меньше ботинок, то они могут оказаться все на одну ногу (10 левых чёрных, 10 левых коричневых или 10 правых чёрных, 10 правых коричневых). Значит, надо взять 21 ботинок.

Ответ: 21 ботинок.

Задача 23.

В 40 кг морской воды будет 40 · 0,05 = 2 (кг) соли. 2 кг соли составляют 2 % от нового количества воды. Значит, новый раствор соли составит 2 : 0,02 = 100 (кг), поэтому надо добавить 100 - 40 = 60 (кг) пресной воды.

Задание 24.

За 60 минут часовая стрелка проходит 1/12 круга, а минутная - полный круг. Значит, за 1 минуту (после часа) угол между часовой

Задание 25.

По записи видно, что выполняется действие умножения:

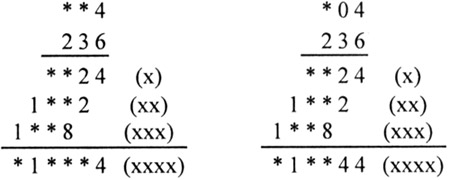
Единиц второго множителя может быть 1 или 6 (только в этом случае может быть 4 единицы в результате). Так как произведение даёт четырёхзначный результат, то 1 не подходит.

Найдём число десятков 1 множителя: 6 · 4 = 24. В строке (х) десятков два, значит, десятков в первом множителе - 0 или 5.

Если взять 5, то в строке (ххх) будет цифра, отличная от нуля и в строке (хххх) не будет 1. Значит, в первом множителе 0 десятков. В строке (ххх) вместо звёздочки может стоять только 0, поэтому число сотен может быть только 5.

Ответ: 504 · 236= 118944.

Задача 26.

Понижение цен на 20 % означает, что новая цена товара равна старой, умноженной на 0,8. Значит, на ту же сумму можно купить товаров в 1: 0,8 = 1,25 (раз) больше, то есть на 25 %.

Задача 27.

Из второго условия следует, что в первом и втором баках должно быть не меньше 26 литров бензина, поэтому их общий объём не меньше 52 литров, что невозможно.

Ответ: невозможно.

Задание 28.

а) Может. Например, путь мухи может быть таким:

ABCDEBFDACFEA.

б) В каждой из восьми вершин куба сходится по три ребра, то есть в каждой из этих вершин муха либо должна начинать свой путь, либо заканчивать, а это невозможно.

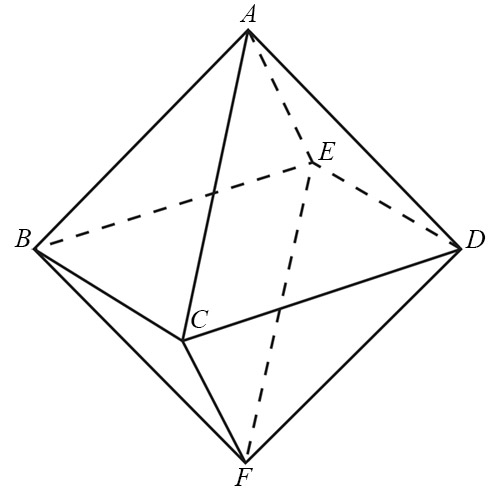
Ответ: в октаэдре - может; в кубе - не может.

Задание 29.

Расположим числа в порядке возрастания. Очевидно, что каждое число не меньше своего номера. Сумма их номеров 1 + 2 + 3 + 4 + 5 + 6 = 21, она на единицу меньше суммы самих чисел. Значит, одно число больше своего номера, а остальные равны ему. Числом, большим своего номера, может быть только последнее число, так как если какое-то число больше своего номера, то все последующие числа тоже больше своего номера. Значит, искомыми числами будут 1, 2, 3, 4, 5, 7.

Задание 30.

За один шаг сумма всех написанных чисел увеличивается на 2. Вначале сумма равна 1, поэтому она всегда будет оставаться нечётной. А сумма четырёх одинаковых чисел, очевидно, чётная. Поэтому добиться того, чтобы все числа стали равными, невозможно.

Ответ: невозможно.

Задание 31.

Если маленький квадрат сдвинуть (без вращения) так, чтобы его центр совпал с центром большого квадрата, то середины всех четырёх отрезков АК, ВМ, СХ и DY сдвинутся (одинаково!) наполовину длины сдвига маленького квадрата. Поэтому если они стали вершинами некоторого квадрата, то и до сдвига они были вершинами некоторого квадрата. Осталось заметить, что если центры квадратов совпадают, то вся «картинка» переходит в себя при поворотах на 90°, 180° и 270°.

Задание 32.

Расположим 3 гири в порядке возрастания и станем раскладывать их по одной на 3 части поочерёдно, то слева направо, то справа налево, то есть после любого чётного числа таких операций (в частности, после 552 : 3 = 184 операций) массы частей будут равны.

Задание 33.

Первый играющий берёт 2 спички первым ходом, а затем дополняет до 4 спичек второго играющего или берёт по 4 спички, если второй берёт по 4 спички.

Задание 34.

Произведя деление «уголком», видим, что 1001 - наименьшее такое число. 1001 : 7 = 143. Следующее такое число получится, если добавить 6 нулей. 1000000001 : 7 = 142857143, то есть число вида 100...01 делится на 7 тогда и только тогда, когда оно содержит 2 + 6n нулей, где n = 0, 1, 2, 3, ... .

Ответ: 2 + 6n нулей, где n = 0, 1, 2, 3, ... .

Задача 35.

Смогут. С 19-го на 96-й этаж: 19 + 7 · 11 = 96; с 96-го на 19-й этаж: 96 + (-9) · 10 = 6; 6 + 7 · 7 = 55; 55 + (-9) · 4 = 19. Указания по проверке: за один первый случай (с 19-го по 96 этаж) - 1 балл.

Задача 36.

Рассмотрим мальчика № 1. Тогда найдутся мальчики (пусть это № 2, № 3, № 4), которые родились с ним в одном месяце. Далее для каждого из мальчиков № 5, № 6, № 7 среди № 1 - № 4 найдётся хотя бы один мальчик, который родился с ним в одном месяце. Значит, все они родились в одном месяце.

Задание 37.

Задание 38.

Если бы напротив круга был круг, то куб не мог бы выглядеть так, как на средней картинке (ибо из любых двух противоположных граней куба одна видна на картинке). Значит, на третьей картинке круг находится либо на левой, либо на нижней грани кубика. Разбираем эти 2 случая (см. рис.).

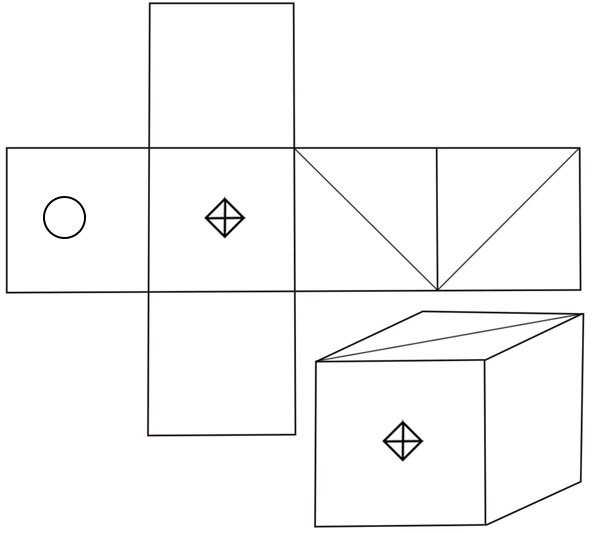
Задача 39.

Пространственная траектория рыбки и вид сверху:

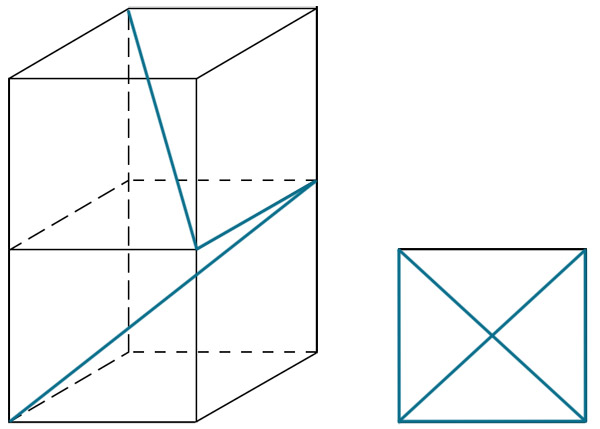
Задание 40.

Один из способов оклейки куба - на рисунке 7. Каждая из невидимых граней оклеивается так же, как и противоположная ей видимая грани.

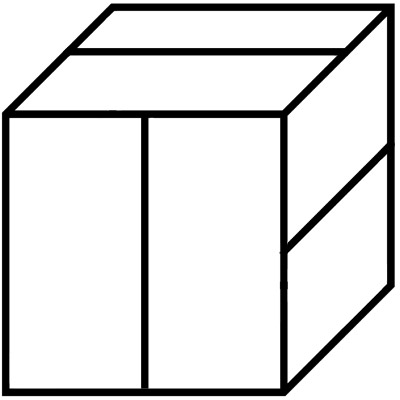
Задача 41.

Три студента заняли 3 первых места, набрав вместе 22 + 21 + 20 = 63 балла. Значит, двое участников набрали: 104 - 63 = 41 (балл). Значит, один из них набрал 21 балл, другой - 20.

Таким образом, они заняли соответственно второе и третье места. Значит, всего одно первое, два вторых и два третьих места.

Ответ: одно первое, два вторых и два третьих места.

Задача 42.

Если количество нечётных чисел нечётное, то можно стереть любое из них. Если же количество нечётных чисел чётное, то на доске есть хотя бы одно чётное число (всего чисел 2005). Его и стираем. Если на доске написаны 2006 нечётных чисел, то сумма их чётная и при стирании любого из них сумма оставшихся чисел будет нечётной.

Задача 43.

Французским языком владеют 100 % - 56 % = 44 % служащих, из них 4 % владеют тремя языками. Ровно двумя языками владеют 37 %, из них 15 % - 4 % = 11 % служащих - английским и немецким; значит, французским и немецким или французским и английским владеют 37 % - 11 % = 26 %. Итого: только французским языком владеют 44 % - 4 % - 26 % = 14 % служащих.

Ответ: 14% служащих.

Задание 44.

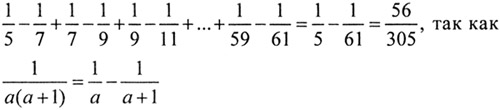
Задание 45.

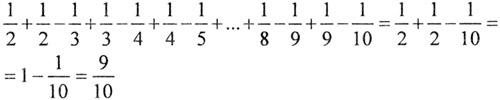
Задание 46.

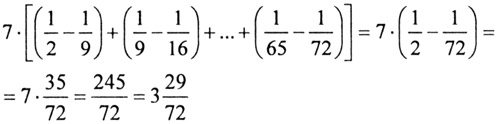
Задание 47.

Раскрасим доску как шахматную. Тогда шашки, стоящие на белых полях, должны попасть на чёрные, а шашки, стоящие на чёрных, - на белые. Но число чёрных полей не равно числу белых, поэтому требуемую перестановку осуществить невозможно.

Ответ: невозможно.

Задача 48.

Если бы в корзине нашлись 12 груздей, то ни один из них не был бы рыжиком, значит, количество груздей не превосходит 11. Если бы груздей было меньше 11, то их было бы не больше 10, а тогда можно было бы найти 20 негруздей (а среди 20 грибов по условию хотя бы один груздь).

Ответ: груздей было 11, а рыжиков - 19.

Задание 49.

Если бы напротив круга был круг, то куб не мог бы выглядеть так, как на среднем рисунке (ибо из любых двух противоположных граней куба одна видна на рисунке). Значит, на третьей картинке круг находится либо на левой, либо на нижней грани кубика. Разберём эти 2 случая.

а) Если круг на левой грани, то единственный способ увидеть одновременно круг, пустую грань и ромбик - посмотреть на кубик третьей картинки снизу слева (двух ромбиков не может быть - в противном случае не найдётся места для треугольников). Но при этом по часовой стрелке мы увидим круг, ромбик и белую грань, а должно быть наоборот: круг, белая грань и ромбик.

б) Во втором случае по той же причине, что и в первом, невозможно увидеть первую картинку, если смотреть справа снизу. Значит, на самом деле белая грань, которую мы видим на первой картинке, расположена слева на третьей картинке. Это означает, что напротив белой грани расположена белая грань, внизу третьей картинки - круг, а на задней грани третьей картинки - треугольник.

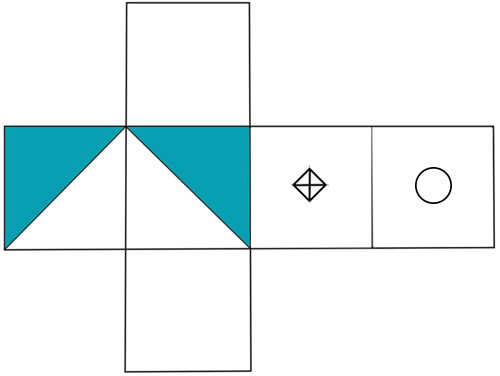
Задача 50.

а) 5 автомобилей, очевидно, не хватит, а 6 - достаточно: нужно только позаботиться о том, чтобы их «выходные» были в разные дни.

б) 9 автомобилей не хватит: в какой-то день недели два из них должны простаивать, так что на ходу только 7 автомобилей, а нужно 8. А 10 автомобилей достаточно: «выходные» можно распределить так, что каждый день будут простаивать не больше двух автомобилей.

Ответ: 6 автомобилей; 10 автомобилей.

Задача 51.

8 кошек, 14 собак и 10 человек.

Задача 52.

Предположим, что количество кусков - 2001. Тогда 1 + 6х + 12у = 2001; 6х + 12у = 2000; 3х + 6у = 1000. Выражение в левой части кратно 3, правая часть не кратна 3. Противоречие.

Ответ: учитель прав.

Задача 53.

У Андрея чёрный мяч; у Димы - красный; у Вити - белый; у Саши - синий.

Задание 54.

Нет. Сумма всех чисел: 1 + 2 + 3 + .. + 8 = 36, а суммы шести последовательных чисел на гранях: n + n + 1 + n + 2 + n + 3 + n + 4 + n + 5 = 6n + 15; 6n + 15 = 36; 6n = 21; n - не целое число.

Задание 55.

От третьей булки отрежем её пятую часть, разрежем её пополам и дадим тем двоим, у кого есть уже половина, то есть 1/2 + 1/10 = 3/5. Оставшуюся часть третьей булки разрежем на 3 равные части и раздадим троим, у которых уже есть по трети булки, каждый получит по 1/3 + 4/15 = 3/5 булки.

Задача 56.

Удар кузнеца молотом можно считать мгновенным. Первый удар он производит в первое мгновение - в первую секунду, а последний - четвёртый - в последнюю, двенадцатую секунду. Значит, за 12 : 3 = 4 (с) он делает один удар (промежуток между двумя ударами). За 24 с он успевает выполнить только 7 ударов. Значит, на нанесение восьми ударов ему потребуется 28 с.

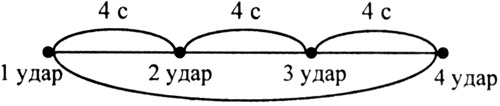
Ответ: 28 секунд.

Рекомендуем посмотреть:

Олимпиадные задачи на тему «Чётность» с ответами, 5 класс

Задачи на «Инвариант» с ответами, 6 класс. Алгебра

Принцип Дирихле. Задачи с решениями 6-7 класс с ответами и решением

Интеллектуальный марафон по математике с ответами, 5-9 класс

Задачи на «Раскраски» олимпиадные с решением