Задачи на «Раскраски» олимпиадные с решением

Математические задачи с решениями. Тема: Раскраски

Говорят, что фигура окрашена в несколько цветов, если каждой точке фигуры приписан определённый цвет. Бывают задачи, где раскраска фигуры уже дана, например, на шахматной доске. Бывают и такие задачи, где раскраску с данными свойствами нужно придумать, а также такие, где раскраска используется в качестве идеи решения.

Задача 1.

Можно ли все клетки доски 9x9 обойти конём по одному разу и вернуться в исходную клетку?

Решение:

Каждым ходом конь меняет цвет клетки, поэтому если существует обход, то число чёрных клеток должно равняться числу белых, что неверно.

Ответ: нельзя.

Задача 2.

В каждой клетке доски в 5 х 5 клеток сидел жук. Затем каждый жук переполз на соседнюю (по стороне) клетку. Докажите, что осталась хотя бы одна пустая клетка.

Решение:

Раскрасим доску в 2 цвета. Чёрных клеток - 13, а белых - 12. При переползании с чёрных клеток жуки переползли на белые и наоборот. Так как белых клеток 12, а чёрных на 1 клетку больше и все жуки с белых переползают на чёрные, то 1 чёрная клетка останется.

Ответ: останется 1 черная клетка.

Задача 3.

Дана доска в 19 х 19 клеток. На каждой клетке поставлено по шашке. Можно ли переставить шашки так, чтобы каждая шашка оказалась на соседней клетке (по горизонтали или по вертикали, но не диагонали)?

Решение:

Раскрасим доску как шахматную. Тогда шашки, стоящие на белых полях, должны попасть на чёрные, а шашки, стоящие на чёрных полях, - на белые. Но число чёрных полей не равно числу белых, поэтому требуемую перестановку осуществить невозможно.

Ответ: нельзя.

Задача 4.

Докажите, что плоскость можно раскрасить девятью красками так, что никакие две точки одного цвета не будут находиться на расстоянии 1 м друг от друга.

Решение:

Разбейте плоскость квадратной сеткой со стороной квадратов 60 см, в квадрате 180 х 180 см квадратики раскрасьте в разные цвета, а потом периодически продолжайте раскраску.

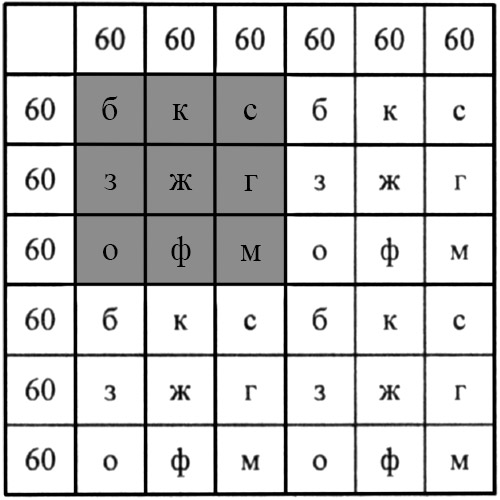
Ответ: можно раскрасить.

Задача 5.

На части шахматной доски размером 3x3 клетки в одной из клеток стоит конь. Можно ли им обойти все девять клеток этой части доски?

Решение:

Если бы это было возможно, то когда-нибудь конь должен был бы попасть в среднюю клетку, но тогда ему вообще некуда ходить на данной части доски, и в эту клетку, значит, он попасть не может.

Ответ: нет.

Задача 6.

Представьте себе, что вам удалось поймать 25 жуков и посадить их по одному на каждую клетку шахматной доски размером 5x5 клеток. Давайте предположим, что каждый жук переполз на соседнюю по горизонтали или вертикали клетку этой части доски. Как вы думаете, останутся ли при этом пустые клетки?

Решение:

Как бы жуки ни переползали, всегда останется пустая клетка. Действительно, назовём чёрными тех жуков, которые сначала сидели на чёрных клетках, а остальных назовём белыми. После того, как каждый жук переполз на соседнюю клетку, все чёрные жуки оказались на белых клетках. Мы имеем 13 чёрных жуков и только 12 белых клеток. Значит, на некоторой белой клетке встретятся по крайней мере 2 жука. Но тогда одна клетка доски останется пустой (ведь число клеток равно числу жуков).

Ответ: останется пустой 1 клетка.

Задача 7.

На каждой клетке доски размером 9x9 клеток лежит фишка. Петя хочет передвинуть каждую фишку на одну из соседних четырёх клеток так, чтобы снова ни одна клетка не осталась пустой. Сможет ли он это сделать?

Решение:

Раскрасим доску в шахматном порядке. Чёрных клеток - 41, белых - 40. При передвижении фишек на соседнее поле меняется цвет поля. Все фишки чёрного цвета (их 41 штука) должны встать на белые поля (а их 40 штук), то есть белых клеток не хватит, и 2 фишки чёрного цвета встанут на одно белое поле.

Ответ: не сможет.

Рекомендуем посмотреть:

Олимпиадные задачи на тему «Чётность» с ответами, 5 класс

Интеллектуальный марафон по математике с ответами, 5-9 класс

Задачи на «Инвариант» с ответами, 6 класс. Алгебра

Принцип Дирихле. Задачи с решениями 6-7 класс с ответами и решением

Задачи на движение 5 класс с решениями и пояснениями