Задачи на движение 5 класс с решениями и пояснениями

Математические задачи для школьников 5-7 класса. Тема: Отрезок, прямая. Задачи на движение

Задача 1.

На прямой через равные промежутки поставили 10 точек, они заняли отрезок длиной a. На другой прямой через такие же промежутки поставили 100 точек, они заняли отрезок длиной b. Во сколько раз а меньше b?

Решение:

Расстояние между соседними точками равно a/9 тогда b = (a/9) · 99, то есть b = 11а.

Ответ: a в 11 раз меньше b.

Задача 2.

Длина гардины 1 м 20 см. На каком расстоянии развешаны на этой гардине 6 колец, если расстояние между ними одинаковое?

Решение:

Шесть колец «разбивают» гардину на 5 промежутков: 120 : 5 = 24 (см)

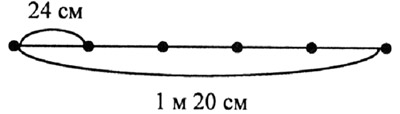
Ответ: на расстоянии 24 см.

Задача 3.

Кузнечик прыгает по прямой большими и малыми прыжками. Большой прыжок составляет 12 см, малый — 7 см. Как ему попасть из точки О в точку А, находящуюся от неё на расстоянии 3 см?

Решение:

12 · 2 – 7 · 3 = 3 (см).

Ответ: кузнечик должен сделать 2 больших прыжка, а потом обратно 3 маленьких.

Задача 4.

Прямоугольник состоит из двух квадратов, имеющих общую сторону. Его периметр равен 12 см. Найти площадь прямоугольника.

Решение:

6х = 12;

х = 2;

S квадрата = 2 · 2 = 4 см²;

S прямоугольника = 2 · 4 = 8 см²

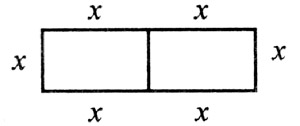
Ответ: площадь прямоугольника 8 см2.

Задача 5.

Проехав треть пути, пассажир лёг спать и спал до тех пор, пока ему не осталось проехать треть того пути, который он проехал спящим. Какую часть всего пути пассажир проехал спящим?

Решение:

Обозначим через х длину отрезка пути, который пассажир проехал после того, как проснулся. Тогда длина отрезка, который он проехал спящим, равна Зх. Так как 4х составляет 2/3 пути, то весь путь равен 6х.

Следовательно, пассажир спал половину пути.

Ответ: пассажир спал половину пути.

Задача 6.

После того, как пешеход прошёл 1 км и половину оставшегося пути, ему осталось пройти треть всего пути и 1 км. Чему равен весь путь?

Решение:

Когда пешеход прошёл 1 км и половину оставшегося пути, ему осталось пройти вторую половину оставшегося пути. Но, с другой стороны, по условию задачи ему осталось пройти треть всего пути и 1 км. Значит, после того, как он прошёл 1 км, его путь составил две трети всего пути и ещё 2 км. Но оставшийся путь на 1 км меньше всего пути. Значит, треть всего пути составляет: 1 + 2 = 3 (км). Весь путь равен 9 км.

Ответ: 9 км.

Задача 7.

Я еду в трамвае и замечаю, что параллельно трамвайной линии в противоположном направлении проходит мой приятель. Через минуту я вышел из вагона и, чтобы догнать его, пошёл вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время я догоню приятеля?

Решение:

Пусть расстояние, которое проходит мой приятель за 1 минуту, есть единица. Тогда расстояние, пройденное мною за 1 минуту, составляет 2 единицы, а расстояние, пройденное трамваем, - 8 единиц. Когда я сошёл с трамвая, расстояние между мною и приятелем составляло: 8 + 1=9 (единиц). Нагоняя приятеля, я каждую минуту сокращал расстояние на 2 - 1 = 1 (единицу). Следовательно, чтобы догнать приятеля, мне потребовалось 9:1=9 (минут).

Ответ: 9 минут.

Задача 8.

Наблюдатель, стоящий на мосту длиной 150 м, заметил, что поезд прошёл мимо него за 10 секунд, а на движение по мосту затратил 25 секунд (считая с момента вступления на мост тепловоза и до момента, когда последний вагон сошёл с моста). Найти длину и скорость поезда.

Решение:

На прохождение расстояния, равного длине поезда, поезд затратил 10 секунд, а на прохождение такого же расстояния плюс 150 м - 25 секунд. Значит, скорость поезда равна: 150 : (25 - 10) = 10м/с = (10·60·60)/1000 = 36км/ч. Длина поезда: 10 • 10= 100 (м).

Ответ: Длина поезда - 100 м, скорость - 36 км/ч.

Задача 9.

Инженер ежедневно приезжает поездом на вокзал в 8 часов утра. Точно в 8 часов к вокзалу подъезжает автомобиль и отвозит инженера на завод. Однажды инженер приехал на вокзал в 7 часов утра и пошёл навстречу машине. Встретив машину, он сел в неё и приехал на завод на 20 минут раньше, чем обычно. Определите показания часов в момент встречи инженера с машиной.

Решение:

По сравнению с обычным своим рейсом машина не проехала на этот раз расстояние от места встречи с инженером до вокзала и обратно - от вокзала до места встречи. Экономия составила 20 минут. Значит, место встречи находилось в 10 минутах езды до вокзала, куда машина должна была прибыть в 8 часов. Следовательно, в момент встречи часы показывали 7 часов 50 минут.

Ответ: показания часов - 7 часов 50 минут.

Задача 10.

Кузнец бьёт молотом по наковальне 4 раза в течение 12 секунд. Сколько ему потребуется времени, чтобы нанести по наковальне 8 ударов?

Решение:

Удар кузнеца молотом можно считать мгновенным. Первый удар он производит в первое мгновение - в первую секунду, а последний - четвёртый - в последнюю, двенадцатую секунду. Значит, за 12 : 3 = 4 (секунды) он делает один удар (промежуток между двумя ударами). За 24 секунды он успевает выполнить только 7 ударов. Значит, на нанесение восьми ударов ему потребуется 28 секунд.

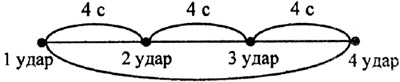
Ответ: 28 секунд.

Задача 11.

Кузнечик прыгает по прямой: первый прыжок на 1 см, второй - на 2 см и т. д. Может ли он после 25-го прыжка вернуться в точку, с которой начал?

Решение:

Чтобы кузнечику после 25-го прыжка оказаться в начальной точке, необходимо преодолеть длину, равную чётному числу. Но это невозможно, так как 1 + 2 + 3 + ... + 13 + ... + 25 = (1 + 25) • 12 + 13 - нечётное число.

Ответ: не может.

Задача 12.

Сколько мостов соединяют 40 островов, если известно, что каждый остров соединяется с остальными островами ровно тремя мостами?

Решение:

На каждом острове имеется 3 конца мостов, следовательно, на всех островах всего 120 концов мостов, самих же мостов будет ровно в 2 раза меньше, то есть 60 мостов.

Ответ: 60 мостов.

Задача 13.

Нарисуйте 8 точек и соедините их отрезками так, чтобы отрезки не пересекались и через каждую точку проходило ровно 4 отрезка.

Ответ:

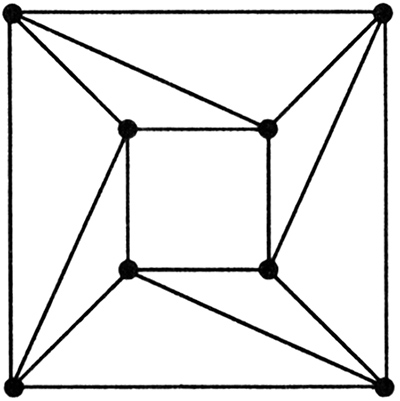
Рекомендуем посмотреть:

Олимпиадные задачи на тему «Чётность» с ответами, 5 класс

Принцип Дирихле. Задачи с решениями 6-7 класс с ответами и решением

Задачи на «Инвариант» с ответами, 6 класс. Алгебра

Задачи на «Раскраски» олимпиадные с решением

Интеллектуальный марафон по математике с ответами, 5-9 класс