Задачи на представление данных с помощью таблиц
Биглова И.И. учитель информатики СОШ №146.
Разработка предназначена учителю информатики при прохождении темы "Информационные модели". В ней рассматриваются примеры решения задач на представление данных с помощью таблиц. Во всех задачах, рассматриваемых в данной работе, используются практически одни и те же таблицы. Однако, формулировки вопросов для нахождения результатов задачи – разные. В литературе, посвященной решению такого рода заданий ЕГЭ, нет большого разнообразия в формулировках задач. Для подготовки учащихся к экзамену необходимы задачи с новыми формулировками. Они помогут сформировать класс задач, который будет достаточен для подготовки ученика к ЕГЭ.
Рассмотрим некоторые из таких задач. Назовем их задачами первого типа. В задачах первого типа дана таблица с данными, которые представляют собой протяженности дорог (или стоимости проезда) между некоторыми населенными пунктами, требуется найти путь (стоимость проезда) между двумя заданными населенными пунктами, удовлетворяющий определенному условию. Во всех задачах такого типа в основном требуется найти кратчайший путь (наименьшую стоимость проезда). Поэтому в данной работе рассматриваются задачи практически с одинаковыми таблицами, но с разными вопросами.
Задача №1
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
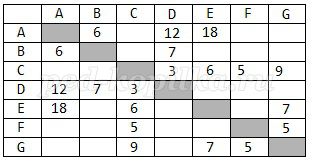Таблица 1
Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).
(Эта задача подобна заданию №5 из демонстрационного варианта 2015 года.)
Исходные данные здесь представлены таблицей. Один из вариантов решения задачи состоит в том, что вначале нужно найти все возможные пути, определить длины этих путей, а затем найти минимальную длину. Самое сложное в этой задаче – не пропустить ни одного пути. Для этого лучше всего наглядно представить схему дорог с помощью графа.
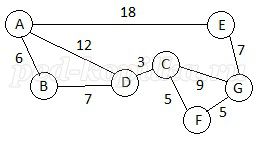Рисунок 1.
Первый путь - AEG. Его длина 18+7=25. Второй путь - путь ADCG. Его длина 12+3+9=24. Третий путь - ADCFG. Его длина 12+3+5+5 = 25. Четвертый путь - ABDCG. Его длина 6+7+3+9 = 25, и наконец, длина пятого пути ABDCFG равна 6+7+3+5+5=26. Наименьшую длину 24 имеет только один путь ADCG.
Задача №2
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (см. таблицу 1 в задаче №1) (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути, проходящего через пункт B, позволяющего проехать из пункта A в пункт G (при условии, что передвигаться можно только по построенным дорогам).
Для решения этой задачи подойдет тот же граф, что и в задаче №1, который изображен на рисунке 1. Всего путей 5 (см. решение задачи №1). Путей, проходящих через вершину B, всего 2. Это пути ABDCG и ABDCFG. Кратчайший из них - ABDCG, его длина равна 6+7+3+9 = 25.
Задача №3
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице (см. таблицу 1 в задаче №1). (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути, позволяющего проехать из пункта A в пункт G, минуя пункт C (при условии, что передвигаться можно только по построенным дорогам).
Для решения задачи в такой формулировке нужно построить новый граф.
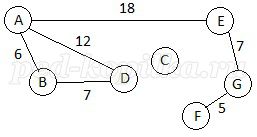Рисунок 2.
При рассмотрении этого графа можно увидеть только один путь, позволяющий проехать из A в G. Это путь AEG. Его длина равна 25.
Во всех этих трех задачах таблицы были одинаковыми, различались только формулировки задачи. Рассмотрим теперь четвертую задачу. В ней будет одно отличие от предыдущих таблиц.
Задача №4
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
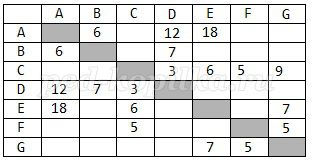Таблица 2.
Определите длину кратчайшего пути, позволяющего проехать из пункта A в пункт G и вновь вернуться в пункт A (при условии, что передвигаться можно только по построенным дорогам).
Сравнивая полученную таблицу с той, которая использовалась ранее, замечаем, что в ней на пересечении строки G и столбца C находится пустая ячейка, которая может означать только одно, что дороги из G в C нет. С другой стороны, в ячейке, находящейся на пересечении строки C и столбца G, находится число 9, которое говорит о том, что дорога из пункта C в пункт G есть и ее длина равна 9. Поэтому для данной задачи можно предположить, что проезд из пункта C в пункт G открыт, а из пункта G в пункт C - нет. Возможно, это связано с ремонтом дорог. Для решения этой задачи построим граф, в котором линии черного цвета используются для отображения путей, следующих из пункта A в пункт G, а линии красного цвета используются для отображения путей, следующих из пункта G в пункт A. Прерывистая линия означает, что такой путь недоступен.
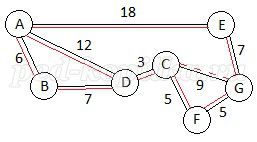Рисунок 3.
Таким образом, прямой путь из пункта A в пункт G может содержать путь из пункта C в пункт G и, следовательно, как и в задаче №1, кратчайший путь – это путь ADCG с длиной, равной 24. Обратный путь из пункта G в пункт A не может содержать путь GC. Таких обратных путей три. Это пути - GEA, GFCDA, GFCDBA. Их длины соответственно равны 25, 25, 26. Наименьших путей – 2. Их длина равна 25. Это означает, что длина кратчайшего пути из пункта A в пункт G и обратно в пункт A составит 24+25=49.
Задача №5
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице (см. таблицу 2 в задаче №4). (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.) В проекте находится построение новой дороги, которая пройдет через населенные пункты B и F, ее протяженность составит 12. При этом временно будет открыта дорога только в одну сторону из пункта F в B. Определите длину кратчайшего пути, позволяющего проехать из пункта A в пункт G и вновь вернуться в пункт A (при условии, что передвигаться можно только по построенным дорогам), если будет открыта эта временная дорога.
Для решения этой задачи построим граф, в котором линии черного цвета используются для отображения путей, следующих из пункта A в пункт G, а линии красного цвета используются для отображения путей, следующих из пункта G в пункт A. Прерывистая линия означает, что такой путь недоступен. На графе прямой линией будет отображен путь из пункта F в B, а прерывистой линией путь из пункта B в F.
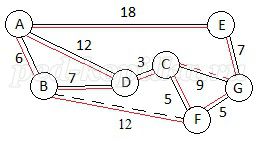Рисунок 4.
Для данной задачи важно знать, что проезда из пункта B в F нет. Значит, в пункт G можно проехать либо через пункт E, либо через пункт С. Поскольку в таблице 2 обозначен только проезд из C в F, то из пункта A в пункт G можно проехать путем ADCG. Его длина составит 12+3+9 = 24. В обратную сторону лучше проехать путем GFDA. Этот путь короче других. Его длина составит 5+12+5 = 22. Общая длина пути из пункта A в пункт G будет равна 24+22=46.
Таким образом, решение задач первого типа формирует умение по нахождению значений параметров задачи и показывает, насколько важно представлять табличные данные взвешенным графом.
Что такое технология потоковых данных
Использование облачного хранилища данных в образовательном пространстве
Восьмеричный переход
Конспект урока информатики по теме «Разветвляющие алгоритмы», 10 класс
Разработка предназначена учителю информатики при прохождении темы "Информационные модели". В ней рассматриваются примеры решения задач на представление данных с помощью таблиц. Во всех задачах, рассматриваемых в данной работе, используются практически одни и те же таблицы. Однако, формулировки вопросов для нахождения результатов задачи – разные. В литературе, посвященной решению такого рода заданий ЕГЭ, нет большого разнообразия в формулировках задач. Для подготовки учащихся к экзамену необходимы задачи с новыми формулировками. Они помогут сформировать класс задач, который будет достаточен для подготовки ученика к ЕГЭ.
Рассмотрим некоторые из таких задач. Назовем их задачами первого типа. В задачах первого типа дана таблица с данными, которые представляют собой протяженности дорог (или стоимости проезда) между некоторыми населенными пунктами, требуется найти путь (стоимость проезда) между двумя заданными населенными пунктами, удовлетворяющий определенному условию. Во всех задачах такого типа в основном требуется найти кратчайший путь (наименьшую стоимость проезда). Поэтому в данной работе рассматриваются задачи практически с одинаковыми таблицами, но с разными вопросами.
Задача №1
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Таблица 1
Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).
(Эта задача подобна заданию №5 из демонстрационного варианта 2015 года.)
Исходные данные здесь представлены таблицей. Один из вариантов решения задачи состоит в том, что вначале нужно найти все возможные пути, определить длины этих путей, а затем найти минимальную длину. Самое сложное в этой задаче – не пропустить ни одного пути. Для этого лучше всего наглядно представить схему дорог с помощью графа.
Рисунок 1.
Первый путь - AEG. Его длина 18+7=25. Второй путь - путь ADCG. Его длина 12+3+9=24. Третий путь - ADCFG. Его длина 12+3+5+5 = 25. Четвертый путь - ABDCG. Его длина 6+7+3+9 = 25, и наконец, длина пятого пути ABDCFG равна 6+7+3+5+5=26. Наименьшую длину 24 имеет только один путь ADCG.
Задача №2
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (см. таблицу 1 в задаче №1) (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути, проходящего через пункт B, позволяющего проехать из пункта A в пункт G (при условии, что передвигаться можно только по построенным дорогам).
Для решения этой задачи подойдет тот же граф, что и в задаче №1, который изображен на рисунке 1. Всего путей 5 (см. решение задачи №1). Путей, проходящих через вершину B, всего 2. Это пути ABDCG и ABDCFG. Кратчайший из них - ABDCG, его длина равна 6+7+3+9 = 25.
Задача №3
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице (см. таблицу 1 в задаче №1). (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути, позволяющего проехать из пункта A в пункт G, минуя пункт C (при условии, что передвигаться можно только по построенным дорогам).
Для решения задачи в такой формулировке нужно построить новый граф.
Рисунок 2.
При рассмотрении этого графа можно увидеть только один путь, позволяющий проехать из A в G. Это путь AEG. Его длина равна 25.
Во всех этих трех задачах таблицы были одинаковыми, различались только формулировки задачи. Рассмотрим теперь четвертую задачу. В ней будет одно отличие от предыдущих таблиц.
Задача №4
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Таблица 2.
Определите длину кратчайшего пути, позволяющего проехать из пункта A в пункт G и вновь вернуться в пункт A (при условии, что передвигаться можно только по построенным дорогам).
Сравнивая полученную таблицу с той, которая использовалась ранее, замечаем, что в ней на пересечении строки G и столбца C находится пустая ячейка, которая может означать только одно, что дороги из G в C нет. С другой стороны, в ячейке, находящейся на пересечении строки C и столбца G, находится число 9, которое говорит о том, что дорога из пункта C в пункт G есть и ее длина равна 9. Поэтому для данной задачи можно предположить, что проезд из пункта C в пункт G открыт, а из пункта G в пункт C - нет. Возможно, это связано с ремонтом дорог. Для решения этой задачи построим граф, в котором линии черного цвета используются для отображения путей, следующих из пункта A в пункт G, а линии красного цвета используются для отображения путей, следующих из пункта G в пункт A. Прерывистая линия означает, что такой путь недоступен.
Рисунок 3.
Таким образом, прямой путь из пункта A в пункт G может содержать путь из пункта C в пункт G и, следовательно, как и в задаче №1, кратчайший путь – это путь ADCG с длиной, равной 24. Обратный путь из пункта G в пункт A не может содержать путь GC. Таких обратных путей три. Это пути - GEA, GFCDA, GFCDBA. Их длины соответственно равны 25, 25, 26. Наименьших путей – 2. Их длина равна 25. Это означает, что длина кратчайшего пути из пункта A в пункт G и обратно в пункт A составит 24+25=49.
Задача №5
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице (см. таблицу 2 в задаче №4). (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.) В проекте находится построение новой дороги, которая пройдет через населенные пункты B и F, ее протяженность составит 12. При этом временно будет открыта дорога только в одну сторону из пункта F в B. Определите длину кратчайшего пути, позволяющего проехать из пункта A в пункт G и вновь вернуться в пункт A (при условии, что передвигаться можно только по построенным дорогам), если будет открыта эта временная дорога.
Для решения этой задачи построим граф, в котором линии черного цвета используются для отображения путей, следующих из пункта A в пункт G, а линии красного цвета используются для отображения путей, следующих из пункта G в пункт A. Прерывистая линия означает, что такой путь недоступен. На графе прямой линией будет отображен путь из пункта F в B, а прерывистой линией путь из пункта B в F.
Рисунок 4.
Для данной задачи важно знать, что проезда из пункта B в F нет. Значит, в пункт G можно проехать либо через пункт E, либо через пункт С. Поскольку в таблице 2 обозначен только проезд из C в F, то из пункта A в пункт G можно проехать путем ADCG. Его длина составит 12+3+9 = 24. В обратную сторону лучше проехать путем GFDA. Этот путь короче других. Его длина составит 5+12+5 = 22. Общая длина пути из пункта A в пункт G будет равна 24+22=46.
Таким образом, решение задач первого типа формирует умение по нахождению значений параметров задачи и показывает, насколько важно представлять табличные данные взвешенным графом.
Рекомендуем посмотреть:
Что такое технология потоковых данных
Использование облачного хранилища данных в образовательном пространстве
Восьмеричный переход
Конспект урока информатики по теме «Разветвляющие алгоритмы», 10 класс
Похожие статьи:
Оценка достижений учащихся на уроках информатики
Конспект открытого урока по информатике в 9 классе
Конспект урока информатики в 8 классе
 |
Автор: Ирина Ивановна Биглова
Опубликовано: 3294 дня назад (12 апреля 2015)
Просмотров: 6327
Блог: Блог Бигловой Ирины
Рубрика: Методические разработки
|
+1↑ Голосов: 1 |
| # 12 апреля 2015 в 16:46 +1 | ||
|
