Использование технологии проблемного диалога на уроках математики

Описание материала: Предлагаю вам статью, в которой показано, как с помощью технологии проблемного диалога можно преодолеть кажущуюся сухость и скучность математики, как увлечь учащихся математикой, стимулировать их учебу, внести в нее эмоции, жажду знаний. Данный материал будет полезен учителям математики и среднего и старшего звена.
Статья по теме «Использование технологии проблемного диалога на уроках математики как инструмента реализации ФГОС».
Во все времена школа боялась реформ, а сейчас – введения ФГОС.
Роль творчества как двигателя прогресса осмыслена уже давно, но лишь недавно психологи и педагоги задумались о том, чтобы сделать творчество движущей силой развития человека. Не удивительно, что центральной стала идея творческого обучения детей в обычной школе. На уроке по любому предмету ученики могут занять позицию «учёных» и открывать новые для себя знания. Технология проблемного диалога представляет собой современную образовательную технологию деятельностного типа – это ключ к успеху в педагогической профессии. Эта технология позволяет заменить урок объяснения нового материала уроком «открытия» новых знаний. Проблемный урок воспитывает активную личность, репродуктивный – пассивную.
Творческие звенья деятельности учащихся на уроке «открытия» нового знания:
1. Постановка учебной проблемы (учащиеся сталкиваются с противоречием и испытывают чувство затруднения или удивления);
2. Поиск решения (мыслительная работа по выдвижению и проверке гипотез);
3. Выражение решения (выражение нового знания в доступной форме);
4. Реализация продукта (представление продукта учителю, классу).
Смысл технологии проблемного диалога заключается в том, чтобы на уроке изучения нового материала «пропустить» школьников через все звенья научного творчества. Проделать такую работу на уроке дети могут только в диалоге с учителем. Поскольку проблема и решение педагогу известны заранее, то он может выбрать вид диалога: побуждающий или подводящий. Побуждающий диалог состоит из отдельных стимулирующих реплик, которые помогают ученику работать по-настоящему творчески. На этапе постановки проблемы этот диалог применяется для того, чтобы ученики осознали противоречие, заложенное в проблемной ситуации, и сформулировали проблему. На этапе поиска решения учитель побуждает учеников выдвинуть и проверить гипотезы, т.е. обеспечивает «открытие» знаний путем проб и ошибок. Подводящий диалог представляет собой систему вопросов и заданий, которая активизирует и, соответственно, развивает логическое мышление учеников. На этапе постановки проблемы учитель пошагово подводит учеников к формулированию темы. На этапе поиска решения он выстраивает логическую цепочку умозаключений, ведущих к новому знанию.
Технология проблемного диалога – это технология, обеспечивающая творческое усвоение знаний учащимися посредством специально организованного учителем диалога. Поэтому перед собой, как педагог, я определила следующую цель - использовать методы и приемы технологии проблемного диалога в преподавании математики для формирования у учащихся личностных, регулятивных, познавательных и коммуникативных универсальных учебных действий.
Личностные УУД. В блок личностных УУД входят жизненное, личностное, профессиональное самоопределение; действия смыслообразования и нравственно-этического оценивания, реализуемые на основе ценнстно-смысловой ориентации учащихся (к готовности к жизненному и личностному самоопределению, знания моральных норм, умения выделять нравственный аспект поведения и соотносить поступки и события с принятыми этическими принципами), а также ориентации в социальных ролях и межличностных отношениях. Традиционное же обучение способствует возникновению пассивной жизненной позиции, нарастанию недовольства учением и школой.
Регулятивные УУД. В блок регулятивных УУД входят действия, обеспечивающие организацию учебной деятельности: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и освоено учащимися, и того, что ещё неизвестно; планирование – определение последовательности промежуточных целей с учётом конечного результата; составление плана и последовательности действий; прогнозирование – предвосхищение результата и уровня усвоения, его временных характеристик; контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона; коррекция – внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона с реальным действием и его продуктом; оценка – выделение и осознание учащимися того, что уже усвоено и что ещё подлежит усвоению. Наконец элементы волевой саморегуляции как способности к мобилизации сил и энергии, волевому усилию – к выбору ситуации мотивационного конфликта, к преодолению препятствий.
Познавательные УУД. В блоке познавательных УУД выделяют:
1. Общеучебные действия: поиск информации, осмысленное чтение, структурирование информации, создание алгоритма деятельности, выбор эффективного способа действия, вычислительные навыки, навыки использования измерительных инструментов;
2. Логические действия: анализ и синтез информации, причинно-следственные связи, выдвижение гипотез, доказательство гипотез, сравнение, классификация, формирование понятия;
3. Знаково-символические действия: Кодирование и декодирование, моделирование, запись информации и её хранение;
4. Постановка и решение проблем: формулирование проблемы, создание способа решения проблемы.
Коммуникативные УУД. В блок коммуникативных УУД входят умения: строить понятные для партнера высказывания, т.е. владеть вербальными и невербальными средствами общения, обосновывать и доказывать свою точку зрения, задавать вопросы, слушать собеседника, позитивно относиться к процессу общения, осуществлять взаимоконтроль и взаимопомощь, иметь навык конструктивного общения, взаимопонимания, планировать общие способы работы, с помощью вопросов получать необходимые сведения от партнера по деятельности, дружить, уступать, убеждать. Рефлексия своих действий (полное отображение предметного содержания и условий осуществляемых действий).
В настоящее время я работаю над методической темой: «Технология проблемного диалога на уроках математики».
Предлагаю рассмотреть приёмы создания проблемных ситуаций, которые можно использовать на уроках введения нового материала в 5 классе (Математика. Арифметика. Геометрия. 5 класс: Учебник. Е.А.Бунимович. Москва «Просвещение», 2014).Вопросы учителя к классу:
1. Чему равна площадь прямоугольника?
(Ответ: площадь прямоугольника равна произведению его смежных сторон)
2. Чему равен периметр прямоугольника?
(Ответ: периметр прямоугольника равен сумме всех его сторон)
3. Вычислите периметр и площадь прямоугольника, если его смежные стороны равны 5см. и 12 см.
(Ответ: 34 см, 60 см2)
4. Вычислите периметр и площадь прямоугольника, если его смежные стороны равны 3/5м. и 4/5м.
(Учащиеся вычислили периметр, однако встретились с проблемой при нахождении площади прямоугольника)
5. Почему вы не смогли вычислить площадь прямоугольника?
(Ответ: не знаем, как умножать дроби)
6. Какая тема урока?
(Ответ: Умножение дробей)
7. Откройте тетради, запишите число и тему урока: Умножение дробей.

На рисунке изображен квадрат со стороной 1м. Стороны этого квадрата разделены на 5 равных частей, квадрат разбит на 25 равных квадратов.
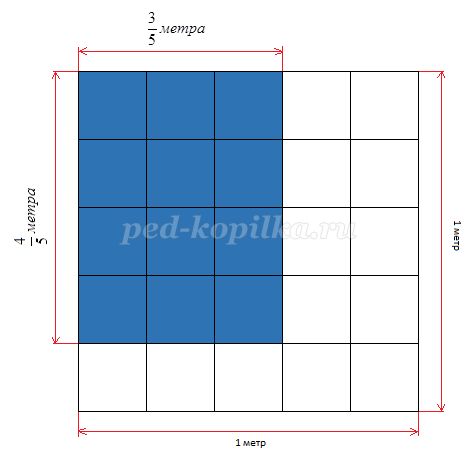
1. Чему равна площадь большого квадрата?
(Ответ: 1 м2)
2. Чему равна площадь маленького квадрата?
(Ответ: 1/25 м^2)
3. Чему равны стороны выделенного прямоугольника?
(Ответ: 4/5 м. и 3/5м.)
4. Как найти площадь прямоугольника?
(Ответ: Умножить длины смежных сторон. Это первый способ: 4/5 ∙ 3/5 ;
Второй способ: сложить площади 12 равных между собой квадратиков – 12/25
5. Какое равенство получилось? Что вы заметили?
(Ответ: 4/5 ∙ 3/5 = 12/25 ; умножили дробь на дробь, формулируют правило)
6. Как записать правило умножения дробей с помощью букв?
7. Запишите правило умножения дробей в общем виде (с помощью букв). Предлагаю учащимся заменить одинаковые цифры в полученных выражениях одинаковыми буквами.
(Ответ: Учащиеся формулируют правило и записывают его с помощью букв: a/b ∙ c/d = (a ∙ c )/(b ∙ d )).Можно предложить учащимся решить следующие задачи двумя способами:
Задача 1. На одной копировальной можно распечатать 6 страниц в минуту, а на другой – 8 страниц. Сколько страниц можно распечатать за 20 минут, если обе машины будут работать одновременно?
Решение.
1 способ. 2 способ.
(6 + 8) · 20 = 280 6 · 20 + 8 · 20 = 280
Ответ: 280 страниц.
Задача 2. Автомобиль и автобус одновременно выехали навстречу друг другу из двух городов. Скорость первой автомобиля 90 км в час, скорость автобуса70 км в час. Через 2 часа они встретились. Какое расстояние между городами, из которых выехали автомобиль и автобус?
Решение.
1 способ. 2 способ.
(90 + 70) ·2 = 320 90 ·2 + 70 · 2 = 320
Ответ: 320 км
Задача 3. Найти площадь прямоугольного участка, состоящего из двух прямоугольных участков.

1 способ. 2 способ.
(5 + 3) · 2 = 16; (5 + 3) · 2 = 16 Ответ: 16 м2
Организовать работу можно как в группах, в парах, так и индивидуально, все это зависит от класса.
После решения всех трёх задач учащимся предлагаю самостоятельно сравнить:
а) первые способы решения задач;
б) вторые способы решения задач;
в) выражения, полученные при решении все трех задач первым способом и вторым способом;
г) выражения, которые были получены при решении конкретной задачи (например, задачи №1);
В результате такого сравнения учащиеся пришли к следующим выводам:
1-й способ решения всех задач одинаков, 2-й – тоже; выражения, полученные при решении задач 1-м (2-м) способом, отличаются друг от друга только числовыми данными. Выражения, полученные при решении задачи №1(№2,№3) 1-м и 2-м способами, отличаются друг от друга числом арифметических действий и порядком действий; числовые значения выражений, полученные при решении задачи №1 (№2, и № 3) 2-мя способами, одинаковы, а, значит, можно сделать такую запись:
(6 +8) 20 =6 20 +8 20;
(90+70) 2 =90 2 +70 2;
(5+3) 2=(5+3) 2.
Далее предлагаю учащимся заменить одинаковые цифры в полученных выражениях одинаковыми буквами. В результате получены три одинаковых выражения, а именно:
(а+в) с=ас + вс.
Потом я говорю:
- Из трёх различных числовых выражений получились три одинаковых буквенных выражения. Встречались ли вы с таким явлением?
- Встречались, - отвечают ученики, - например, при записи переместительного закона умножения.
- И в том случае, - продолжаю я, - мы получили новый закон умножения: распределительный закон умножения относительно сложения.
Ученики с моей помощью формулируют этот закон словесно и на примерах убеждаются в целесообразности усвоения и запоминания этого закона: он облегчает вычисления.
При изучении: правила умножения дробей и распределительного закона умножения относительно сложения был организован подводящий диалог.
Какие же познавательные универсальные учебные действия формируются? Это, прежде всего: анализ текстов задачи; структурирование информации в тексте задачи; определение способов решения задачи; сравнение; обобщение; перевод из одной знаковой системы в другую (из числового выражения в буквенное).При изучении этой темы учащимся необходимо выдвинуть гипотезу, проверить её и сформулировать выводы.
На доске записаны числа: 111, 212, 36, 522, 882, 913, 72, 834. Предлагаю учащимся не из предложенных чисел непосредственным делением, найти те, которые делятся на 3 и на 9.
Затем предлагаю самостоятельно написать несколько многозначных чисел, делимость которых на 3 и на 9 они могут предугадать.
После того как, учащиеся выполнят эту работу, я предлагаю им попытаться найти признаки делимости чисел на 3и на 9.
После того как учащиеся попытаются сформулировать признаки, предлагаю им высказать своё мнение: стоит ли этим заниматься? Не проще ли разделить?
После высказывания предположений организуется сопоставление с учебником, и формулируются окончательные выводы, которые записываются в форме таблицы:

При работе над этими заданиями мною был организован побуждающий диалог.
Какие же познавательные универсальные учебные действия формируются при выполнении данного задания? Это, прежде всего, анализ предложенной информации; выдвижение гипотезы, доказательство гипотезы; структурирование информации; поиск информации в учебнике (справочниках).
Уместно вспомнить китайскую притчу: «Услышал – забыл, увидел – запомнил, сделал сам – понял». Проблемный характер изложения учебного материала, организация поисковой, познавательной деятельности учащихся, даёт им возможность переживать радость самостоятельных открытий, формирует универсальные учебные действия.
Е.А.Бунимович. Математика. Арифметика. Геометрия. 5 класс. Учебник. Москва «Просвещение» 2014
Е.Л.Мельникова. Технология проблемного диалога: методы, формы, средства обучения /Е.Л.Мельникова// Образовательные технологии: сб. мат. – Москва «Баласс», 2008

Рекомендуем посмотреть:

Урок математики по теме Диаграммы в 6 классе Игра "Поле чудес" по математике для учащихся 5-6 классов коррекционных школ VIII вида Внеклассное мероприятие по математике для учащихся коррекционных школ VIII вида Конспект урока математики в 5 классе «Путешествие в страну Математики»

Похожие статьи:

Игра как средство интерактивного обучения по предмету Математика

Конспект урока математики в 6 классе по теме: Умножение и деление обыкновенных дробей

Внеклассное мероприятие по математике для учащихся 7-8 класса. Игра «Слабое звено»

Конспект урока математики 9 класс по теме: Арифметическая и геометрическая прогрессии

Конспект урока математики в 5 классе по теме: Умножение и деление десятичных дробей на натуральные числа