Опыт работы учителя математики. Привлечение учащихся к изучению теоретического материала

Один из путей привлечения учащихся к изучению теоретического материала

Автор: Нейман Алина Абрамовна, учитель математики МОУ "Школа № 20 г. Донецка"
Цель:поделиться опытом проведения контролирующих мероприятий относительно усвоения изучаемого теоретического материала.
Задачи:
• мотивировать целесообразность предлагаемых подходов;
• раскрыть содержание составляющих мероприятия;
• предложить пути реализации этих составляющих;
• привести примеры такой реализации.
Целевая аудитория:учителя математики.
Оборудование:
- компьютер,
- мультимедийный проектор.

Ход занятия

Математика может быть
занимательной,
математические фокусы –
впечатляющими,
математические задания –
увлекательными.
И. В. Гёте
Контрольная работа по теории
Современные критерии оценивания учебных достижений учащихся предусматривают оценивание уровня теоретических знаний. Тематическая контрольная работа дает определенное представление об этом уровне. Но она не способна обнаружить весь спектр характеристик этой подготовки: полноты, глубины, конкретности, обобщенности и т. п. Поэтому желательной является отдельная диагностическая процедура для выявления этих характеристик. В условиях личностно-ориентированного обучения возникает проблема учета и оценивания самостоятельной дополнительной деятельности учеников — овладения знаниями. Такую диагностическую работу естественно назвать математическим сочинением. Название необычно для обучения математике. Но оно довольно правильно отображает назначение этого средства диагностики.

Главными заданиями написания математического сочинения являются контроль за усвоением теоретического материала, предоставление учащимся возможности обнаружить свои склонности, оценить результаты самостоятельной работы, в частности, над дополнительным учебным материалом.

На контрольную работу по теории выносятся узловые учебные вопросы темы. Но ее написание заключается не в простом воспроизведении теоретического материала, а в системном изложении учебного материала по определенному плану. Формирование тем произведений и разработка планов их написания является сложным дидактическим заданием. Количество тем сочинений должно быть небольшим (3 — 6 на одну учебную тему). В совокупности содержание тем сочинений должно охватывать основной теоретический материал. Желательно, чтобы несколько тем, если не все, имели общий обобщенный план.

План написания сочинения способствует систематизации и структуризации теоретического материала. Он должен приучать учащихся к общим схемам изложения учебного материала:
• обоснование необходимости и естественности рассматриваемого понятия;
• иллюстрация содержания понятия, его сущности с помощью примеров и контрпримеров, изложение связей с другими понятиями;
• различение видов теорем (свойств, признаков, теорем существования и т. п.);
• логическая последовательность изложения теоретического материала;
• обоснованность изложения теоретического материала.

Планы написания сочинений разрабатывает учитель вместе с учащимися в течение обучения. Эта деятельность способствует изучению теоретического материала, его систематизации и структуризации, обеспечивает целенаправленность и действенность его усвоения.

Первые такие математические сочинения по теории желательно предлагать учащимся в качестве домашних заданий в начале изучения темы к моменту окончания изучения темы или во время итогового повторения изученного курса за год. Впоследствии контрольную работу по теории целесообразно проводить перед тематической контрольной работой. На ее проведение в зависимости от характера темы можно отводить от 30 до 45 минут. Учащимся разрешается пользоваться конспектами, учебниками, другой справочной литературой.

Оценивание математических сочинений осуществляется по таким показателям:
• полнота выполнения плана;
• уровень обоснованности изложения;
• содержательность и самостоятельность изложения.

В целом оценивается уровень компетентности усвоения, то есть такого усвоения, которое свидетельствует о понимании усвоенного, сознательности усвоения, способности применить учебный материал для разных целей: теоретических, практических. Оценивание должно поощрять учеников к выявлению своей точки зрения, эмоционального отношения.

Конечно, характер тем и планы их написания могут быть разными. Важно лишь, чтобы они обеспечивали сознательное усвоение теоретического материала.

Стоит подчеркнуть, что учащиеся сначала еще не владеют навыками написания математических сочинений, потому их проверка и оценивание должны носить крайне доброжелательный характер. Особое внимание при оценивании следует обратить на полноту раскрытия темы, аргументированность изложения.

Подведение итогов написания математического сочинения целесообразно сопровождать общим анализом состояния усвоения учебного материала, анализом типичных недостатков. Это дает возможность еще раз акцентировать внимание учащихся на ключевых понятиях и фактах темы. Зачитывание удачных фрагментов сочинений учащихся, которые имеют яркие особенности, способствует формированию эмоционального отношения к обучению. Следует также поддерживать желание учащихся исправлять недостатки и отстаивать результаты своей работы.

Примеры тем математических сочинений для 7 класса
Алгебра.
Тема. Функции
Темы сочинений:
• Функция
• Линейная функция
• Прямая пропорциональность
Примерный план
1. Что называется функцией [линейной функцией; прямой пропорциональностью]?
2. Реальные явления, которые описываются функцией [линейной функцией; прямой пропорциональностью].
3. Понятия аргумента функции, ее значения.
4. Вычисление значений функции по заданному аргументу.
5. Нахождение аргумента по заданному значению функции.
6. График функции [линейной функции; прямой пропорциональности].
7. Область определения функции.
8. Смысл параметров k и b в формуле у = kх + b.
9. Чтение графика функции [линейной функции; прямой пропорциональности].
10. Физические процессы, описываемые функциями [линейными функциями; прямой пропорциональностью].

Тема. Степень с натуральным показателем
Темы сочинений:
• Умножение степеней
• Деление степеней
• Возведение степени в степень
Примерный план
1. Определение степени с натуральным показателем.
2. Пример ситуации, в которой возникает необходимость возводить в степень с натуральным показателем.
3. Как выполняется действие умножения степеней [деления степеней, возведения степени в степень]?
4. Степень результата арифметических действий над числами.

5. Как возведение в степень упрощает устные вычисления?
6. Доказательство указанных правил.
7. Для всех ли чисел справедливы эти правила?
8. Картина Н. П. Богданова-Бельского «Устный счет».
9. Рассуждение «Нужны ли степени с отрицательными показателями? С дробными показателями?».

Геометрия
Тема. Треугольник
Темы сочинений:
• Треугольник
• Равнобедренный треугольник
• Прямоугольный треугольник
Примерный план
1. Определение треугольника [равнобедренного треугольника, прямоугольного треугольника]. Характеристика сторон и углов.
2. Периметр треугольника [равнобедренного треугольника, прямоугольного треугольника].
3. Равенство треугольников.
4. Медианы, биссектрисы, высоты.
5. Какие реальные объекты имеют форму треугольника [равнобедренного треугольника, прямоугольного треугольника]?
6. Жесткость треугольника.
7. Является ли равносторонний треугольник равнобедренным? А наоборот?
8. Приведите примеры определений и теорем по теме треугольник [равнобедренный треугольник, прямоугольный треугольник].
9. Выберите утверждение, которое бы вы хотели и могли доказать по теме треугольник [равнобедренный треугольник, прямоугольный треугольник].
10. Физические объекты, которые описываются треугольниками [равнобедренными треугольниками, прямоугольными треугольниками].

Тема. Начальные геометрические сведения
Темы сочинений:
• Угол
• Отрезок
Примерный план
1. Определение угла. Виды углов. Биссектриса угла. [Определение отрезка. Концы отрезка. Середина отрезка].
2. Равенство углов [отрезков].
3. Сравнение углов [отрезков].
4. Действия над углами [отрезками].
5. Измерение углов [отрезков].
6. Единицы измерения углов [отрезков].
7. Измерительные инструменты.
8. Измерение углов на местности.
9. Смежные и вертикальные углы.
10. Физические объекты, которые описываются углами [отрезками].

Пример математического сочинения
Линейная функция
По мотивам рассказа Н. Носова «Мишкина каша»
Один раз, когда я жил с мамой на даче, ко мне в гости приехал Мишка. Я так обрадовался, что и сказать нельзя! Я очень по Мишке соскучился. Мама тоже была рада его приезду.
- Это очень хорошо, что ты приехал, - сказала она. - Вам вдвоём здесь веселей будет. Мне, кстати, завтра надо в город поехать. Я, может быть, задержусь. Проживёте тут без меня два дня?
- Конечно, проживём, - говорю я. - Мы не маленькие!
- Только вам тут придётся самим обед готовить. Сумеете?
- Сумеем, - говорит Мишка. - Чего там не суметь!
- Ну, сварите суп и кашу. Кашу ведь просто варить.
- Сварим и кашу. Чего там её варить! - говорит Мишка.
Наутро мама уехала, а мы с Мишкой решили забраться на чердак, где, как мы знали, стоит большая коробка со старыми детскими игрушками. Чего там только не было! И вот среди всех многочисленных ребячьих сокровищ мы обнаружили термометр для воды.
Таким мамы пользуются, когда собираются купать совсем маленьких детей. Конечно же, мы с Мишкой сразу захотели его опробовать. Да и есть захотелось, пора кашу варить.
Растопили плиту. Я за печкой смотрю, дрова подкладываю, а Мишка пошел к колодцу набрать ведро воды. (Тут всё прошло хорошо, без приключений, не так, как в рассказе!)
А вода-то в колодце холодная! Измерили ее температуру, оказалось, всего 6°С! Налили немного воды в кастрюлю, поставили ее на плиту - мы-то знаем, что крупу надо в кипящую воду засыпать
Сидим, ждем, когда вода закипит, а сами время засекаем – смотрим, на сколько градусов будет повышаться температура за 1 минуту. Целых 10 минут проводили измерения, а потом нам надоело…. Увидели, что через 1 минуту термометр показал 8°С, через 2 минуты - 10°С, еще через минуту - 12°С. А через 10 минут - 26°С. Так мы узнали, что при нагревании температура воды повышалась каждую минуту на 2°С. И тут я вспомнил, что мы как раз в 7 классе на уроках алгебры изучали тему «Функции». И говорю Мишке:
- А ведь если температура воды зависит от времени нагревания, в каждый момент времени вода имеет определенную температуру, то это и есть функциональная зависимость! Здесь время t является независимой переменной, или аргументом, а температура Т воды зависит от времени нагревания, то есть T = T(t) - функция.
Мишка продолжил мои рассуждения:
- И при этом каждую минуту температура повышается на одну и ту же величину. А давай попробуем найти формулу, выражающую изменение температуры Т воды в зависимости от времени t её нагревания. Мы ведь знаем начальную температуру воды, знаем, как она меняется в зависимости от времени.
Немного порассуждав, мы пришли к выводу, что искомая формула должна иметь вид Т(t) = 6 + 2t, где 6°С – температура воды в начале нагревания, 2°С – повышение температуры воды каждую минуту при нагревании, Т – изменение температуры воды (°С), t – время нагревания воды (в минутах).
Мы так обрадовались, что сумели ответить на свой же вопрос, что начали вспоминать уроки алгебры дальше. А какие функции мы уже выучили в школе? Вспомнили линейную функцию и прямую пропорциональность. Стали думать, является ли наша функция линейной. Мишка вспомнил, что линейную функцию можно задать формулой вида y = kx + m , где x — независимая переменная, k и m — некоторые числа. Переписали нашу формулу в виде Т(t) = 2t + 6 и убедились, что Т(t) является линейной функцией.
Потом я предложил Мишке:
- Давай проверим по формуле, какой должна получиться температура воды через 10 минут.
Подставили в формулу t = 10, получили Т(10) = 2•10 + 6 = 26(°С) и полученным результатом остались очень довольны.
Пока мы совместно вспоминали наши знания по теме «Функции», прошло еще 20 минут, и даже больше… Взглянув на наш термометр и убедившись, что он рассчитан только на температуру до + 50°С, опускать его в кастрюлю мы не рискнули. А когда вычислили Т(31), похвалили себя за предусмотрительность, потому что Т(31) = 2•31 + 6 = 68(°С).
И тут Мишка спрашивает:
- Когда уже наша вода закипит, чтоб можно было крупу в кастрюлю засыпать? Есть уже сильно хочется!
Я ему отвечаю:
- Ты сам можешь посчитать. Температуру кипения воды знаешь?
- Знаю, 100°С.
- Вот и узнай с помощью формулы, через сколько минут после начала нагревания вода закипит.
- Так это легко, - обрадовался Мишка и начинает считать.
100°С – температура кипения воды, Т(t) = 2t + 6, получаем:
100 = 6 + 2t,
2t = 94,
t = 47.
Значит, 47 мин – время закипания воды. Уже скоро вода закипит, мы ее посолим, засыплем крупу в кипяток, и через 20-30 минут наша каша будет готова.
- Мишка, - говорю, - ты специалист по графикам? Давай построим график нашей линейной функции! Ты ведь помнишь, какая линия является ее графиком?
- Конечно, помню! График – прямая. Функция потому и называется линейной, что ее график – прямая линия. А прямую можно построить всего по двум точкам.
Мы перенесли уже известные нам данные в таблицу и построили прямую:
t 0 10
T(t) = 2t + 6 6 26
Сидим, ждем, когда вода закипит, а сами время засекаем – смотрим, на сколько градусов будет повышаться температура за 1 минуту. Целых 10 минут проводили измерения, а потом нам надоело…. Увидели, что через 1 минуту термометр показал 8°С, через 2 минуты - 10°С, еще через минуту - 12°С. А через 10 минут - 26°С. Так мы узнали, что при нагревании температура воды повышалась каждую минуту на 2°С. И тут я вспомнил, что мы как раз в 7 классе на уроках алгебры изучали тему «Функции». И говорю Мишке:
- А ведь если температура воды зависит от времени нагревания, в каждый момент времени вода имеет определенную температуру, то это и есть функциональная зависимость! Здесь время t является независимой переменной, или аргументом, а температура Т воды зависит от времени нагревания, то есть T = T(t) - функция.
Мишка продолжил мои рассуждения:
- И при этом каждую минуту температура повышается на одну и ту же величину. А давай попробуем найти формулу, выражающую изменение температуры Т воды в зависимости от времени t её нагревания. Мы ведь знаем начальную температуру воды, знаем, как она меняется в зависимости от времени.
Немного порассуждав, мы пришли к выводу, что искомая формула должна иметь вид Т(t) = 6 + 2t, где 6°С – температура воды в начале нагревания, 2°С – повышение температуры воды каждую минуту при нагревании, Т – изменение температуры воды (°С), t – время нагревания воды (в минутах).
Мы так обрадовались, что сумели ответить на свой же вопрос, что начали вспоминать уроки алгебры дальше. А какие функции мы уже выучили в школе? Вспомнили линейную функцию и прямую пропорциональность. Стали думать, является ли наша функция линейной. Мишка вспомнил, что линейную функцию можно задать формулой вида y = kx + m , где x — независимая переменная, k и m — некоторые числа. Переписали нашу формулу в виде Т(t) = 2t + 6 и убедились, что Т(t) является линейной функцией.
Потом я предложил Мишке:
- Давай проверим по формуле, какой должна получиться температура воды через 10 минут.
Подставили в формулу t = 10, получили Т(10) = 2•10 + 6 = 26(°С) и полученным результатом остались очень довольны.
Пока мы совместно вспоминали наши знания по теме «Функции», прошло еще 20 минут, и даже больше… Взглянув на наш термометр и убедившись, что он рассчитан только на температуру до + 50°С, опускать его в кастрюлю мы не рискнули. А когда вычислили Т(31), похвалили себя за предусмотрительность, потому что Т(31) = 2•31 + 6 = 68(°С).
И тут Мишка спрашивает:
- Когда уже наша вода закипит, чтоб можно было крупу в кастрюлю засыпать? Есть уже сильно хочется!
Я ему отвечаю:
- Ты сам можешь посчитать. Температуру кипения воды знаешь?
- Знаю, 100°С.
- Вот и узнай с помощью формулы, через сколько минут после начала нагревания вода закипит.
- Так это легко, - обрадовался Мишка и начинает считать.
100°С – температура кипения воды, Т(t) = 2t + 6, получаем:
100 = 6 + 2t,
2t = 94,
t = 47.
Значит, 47 мин – время закипания воды. Уже скоро вода закипит, мы ее посолим, засыплем крупу в кипяток, и через 20-30 минут наша каша будет готова.
- Мишка, - говорю, - ты специалист по графикам? Давай построим график нашей линейной функции! Ты ведь помнишь, какая линия является ее графиком?
- Конечно, помню! График – прямая. Функция потому и называется линейной, что ее график – прямая линия. А прямую можно построить всего по двум точкам.
Мы перенесли уже известные нам данные в таблицу и построили прямую:
t 0 10
T(t) = 2t + 6 6 26

Посмотрев на график, Мишка говорит:
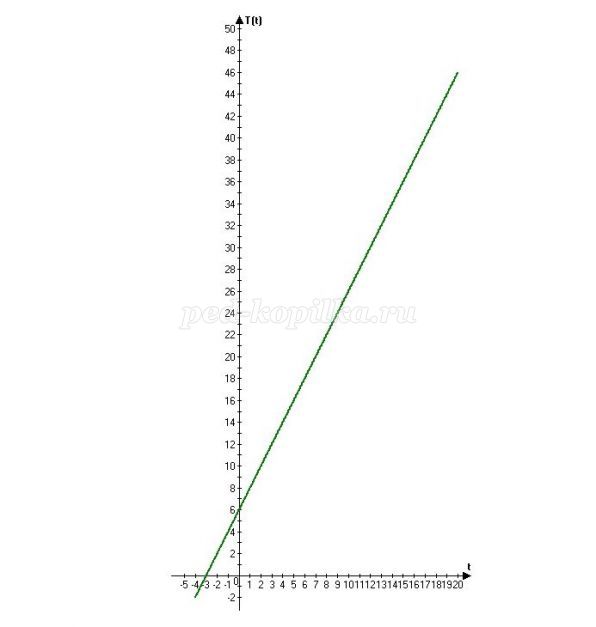
- Что-то в нашем графике не так… Разве может время быть меньше нуля? Это в общем виде и аргумент линейной функции, и ее значение могут быть любым числом. В нашем случае аргумент t не может принимать отрицательные значения. А значения функции Т(t) находятся между 6°С и 100°С.
Пришлось исправлять график:

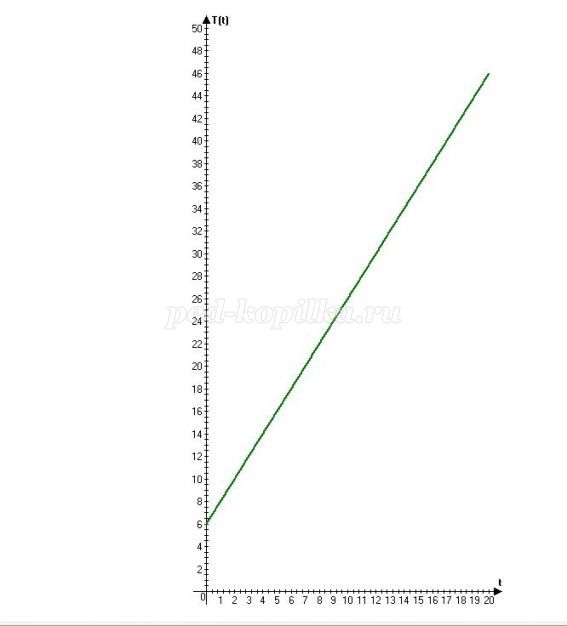
Полюбовались мы своим рисунком. А тут и вода закипела. Посолил Мишка воду, засыпал крупу в кастрюлю и говорит:
- Ну, теперь каша скоро готова будет. Слушай, а если бы мы добавили в печку дров? И температура воды бы за минуту не на 2°С повышалась, а на 3°С. Вода бы, наверное, быстрее закипела.
Записали мы новую формулу: Т(t) = 3t + 6, решили еще одно уравнение:
3t + 6 = 100,
3t = 94.
- Да, - отвечаю я, - вода бы закипела раньше, понадобилось бы чуть больше 31 минуты, и каша бы готова была быстрее…
- А можем мы еще придумать примеры явлений из жизни, которые описываются линейными функциями?
- Да это легко! Расстояния, которые проезжают машины, поезда или проходят пешеходы при определенной скорости движения. Это и есть линейные функции времени движения.
- Зависимость длины окружности от длины её радиуса тоже линейная функция.
- А еще мы по физике закон Гука изучали.
- И даже в литературе есть линейные зависимости! Точнее, в устном народном творчестве.
И чтобы не было скучно ожидать, пока сварится каша, мы с Мишкой стали вспоминать пословицы и поговорки, в которых встречаются линейные зависимости:
- Чем дальше в лес, тем больше дров (прямая пропорциональность y = kx, k > 0).
- Много снега - много хлеба (прямая пропорциональность y = kx, k > 0).
- Дальше в спор - больше слов (прямая пропорциональность y = kx, k > 0).
- Больше почёт, больше хлопот (прямая пропорциональность y = kx, k > 0).
- Как аукнется, так и откликнется (прямая пропорциональность y = x).
- Долго думал, да ничего не выдумал (линейная функция y = b, k = 0).
Вот сколько пословиц вспомнили!
А тут и каша подоспела. Едим мы кашу, нахваливаем.
Неугомонный Мишка продолжает:
- Какие мы молодцы – сами кашу сварили! Только теперь наша каша остывать стала. Пусть за 1 минуту она остывает на 1°С. А какая теперь получилась зависимость температуры каши от времени?
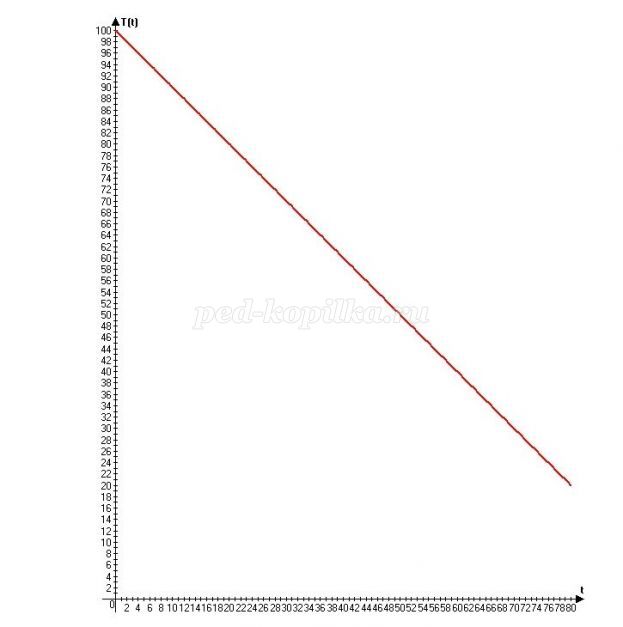
- Конечно, тоже линейная функция, странный вопрос! Если каша остывает, то k<0. Так как скорость остывания каши 1°С в минуту, то k = -1. Начальная температура была 100°С, поэтому b = 100. Отсюда формула, описывающая зависимость температуры каши от времени остывания:
T(t) = 100 – t, - уверенно отвечаю я.
Даже график нарисовать могу! Теперь я эту тему хорошо знаю!

Вот так мы с Мишкой и кашу сварили, и алгебру повторили.

Выводы
Проводить подобные контрольные работы по теории очень непросто. Введенная форма проведения контроля в виде сочинения призвана сделать изучение теоретического материала более привлекательным.
Проведение контрольной работы по теории в виде математического сочинения должно отвечать следующим требованиям:
1. Вначале такие задания предлагать учащимся в качестве домашних. Причем не на следующий урок, а предложить варианты тем заранее, в начале изучения темы.
2. Находить по 5 – 10 минут на уроках, чтобы вместе с учащимися составлять план сочинения. Это будет способствовать более осознанному подходу к изучению теории.
3. Оценивать сочинения учащихся только высокими баллами. Неудачные работы не оценивать совсем.
4. Лучшие работы (либо их фрагменты) желательно зачитывать всем учащимся.
5. Полезно собирать комплекты из лучших сочинений.
Со временем можно переходить к тому, чтобы эти сочинения учащиеся писали на факультативах, занятиях кружка, а в дальнейшем и на уроках.
Есть надежда, что предлагаемая форма работы будет способствовать тому, что учащиеся будут чаще читать учебник. И в результате постепенно будет меняться отношение школьников к изучению теории.

Список литературы
1. Алгебра. 7 класс : учеб. для общеобразоват. организаций / [Ю. Н. Макарычев и др.]; под ред. С. А. Теляковского. – М.: Просвещение, 2016. – 256 с. : ил.
2. Афанасьева О. Н. и др. Книга для учителя. – Т. : Богдан, 2013. – 304 с.
3. Геометрия. 7 – 9 классы : учеб. для общеобразоват. организаций / [Л. С. Атанасян и др.] – М.: Просвещение, 2016. – 383 с. : ил.
4. Мишкина каша : рассказы / Н. Н. Носов; вступ. сл. О. Корф; худож. И. Семёнов, - М. : Махаон, Азбука – Аттикус, 2016. – 112 с. : ил. – (Чтение – лучшее учение).

Скачать Один из путей привлечения учащихся к изучению теоретического материала

Скачать эту работу

Опыт работы учителя математики. Привлечение учащихся к изучению теоретического материала

Рекомендуем посмотреть:

Похожие статьи: