Конспект урока геометрии 10 класс по теме: Симметрия в пространстве. Симметрия в природе и на практике
Конспект урока по геометрии 10 класс
Тема: Симметрия в пространстве. Симметрия в природе и на практике.
Автор: Бурганова Лилия Фаритовна, ГБПОУ «Атнинский сельскохозяйственный техникум им.Габдуллы Тукая»,
с.Большая Атня Атнинского района Республики Татарстан
Описание работы: Конспект урока по дисциплине Математика для 10 класса на тему: Симметрия в пространстве. Симметрия в природе и на практике
Назначение материала: Данный конспект разработан для проведения урока математики в 10-11 классе, материал будет полезен учителям математики старших классов при планировании уроков.
Цель:
Познавательная: обобщение и систематизация знаний по теме «Симметрия на плоскости»; усвоение обучающимися знаний о симметрии в пространстве, преобразования симметрии в пространстве.
Воспитательная: пробуждение устойчивого интереса к предмету и активизации познавательной деятельности обучающихся;
воспитание интереса к своей профессии;
Развивающая: развитие любознательности учащихся, познавательного интереса; развитие памяти; развитие способности обобщать.
Задачи: формировать интерес к изучаемой дисциплине,развивать
общеинтеллектуальные умения: сравнение, анализ, обобщение.
Дидактический материал и оборудование: компьютер, мультимедийный проектор, учебник В.А.Гусев «Математика», А.Н.Погорелов «Геометрия», раздаточные материалчы (тесты)
Ход урока.
I.Организационный момент.Настрой на урок.Проверка готовности группы к уроку и приветствие всех присутствующих.II.Актуализация знаний учащихся. Ознакомление с порядком проведения урока, рекомендации обучающимся, на что необходимо обратить особое внимание, что следует записать в рабочую тетрадь.
Преподаватель предлагает угадать тему урока, ответив на вопросы (ответ: симметрия).
1.Раздел геометрии, в котором изучаются фигуры в пространстве. (Стереометрия)
2.Преобразование пространства, сохраняющее расстояние между соответствующими точками.(Изометрия)
3.Фигура, образованная простой замкнутой ломаной и ограниченной ею частью плоскости, называется…(Многоугольник)
4.«Геометрическое тело», поверхность которого состоит из многоугольников называется…(Многогранником)
5.Через две пересекающиеся прямые проходит…плоскость.(единственная)
6.Утверждения, которые необходимо доказать, называются…(Теорема)
7.Как называются два двугранных угла, если они имеют одну и ту же величину?(равными)
8.Плоскости, которые… хотя бы одну общую точку, называются пересекающимися.(имеют)
9.Что вы видите на рисунке? (Прямая)
Преподаватель: «Наш урок посвящен интересной и увлекательной теме раздела геометрии «Симметрия в пространстве». Мы с вами рассмотрим сегодня также симметрию в природе и на практике.
Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека, и употреблялось скульпторами ещё в V веке до н. э.
Слово «симметрия» греческое. Оно означает «соразмерность», «пропорциональность», одинаковость в расположении частей. Его широко используют все без исключения направления современной науки.
Об этой закономерности задумывались многие великие люди. Например, Л.Н.Толстой говорил: «Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия приятна глазу? Что такое симметрия? Это врождённое чувство. На чём же оно основано?»
Сегодня на уроке постараемся ответить на вопросы, которые поставил перед нами Толстой.
Для начала вспомним с вами из курса основной школы такие понятия, как симметрия относительно точки, симметрия относительно прямой, симметрия относительно оси.
Далее рассмотрим симметрию в пространстве, в природе и на практике.
1. Две точки называются симметричными относительно данной точки (центра симметрии) или центрально симметричными, если данная точка является серединой соединяющего их отрезка.
Центральная симметрия - отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О .
Примеры центральной симметрии
Геометрические фигуры, обладающие центральной симметрией
Точки А1 и А2 пространства называются симметричными относительно прямой l, если прямая l проходит через середину отрезка АА1 и перпендикулярна этому отрезку.Прямая l при этом называется осью симметрии точек А1 и А2
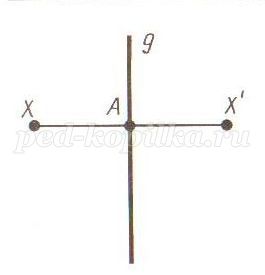
Фигура называется симметричной относительно прямой l, если для каждой точки фигуры симметричная ей точка относительно прямой l также принадлежит этой фигуре. Прямая l называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
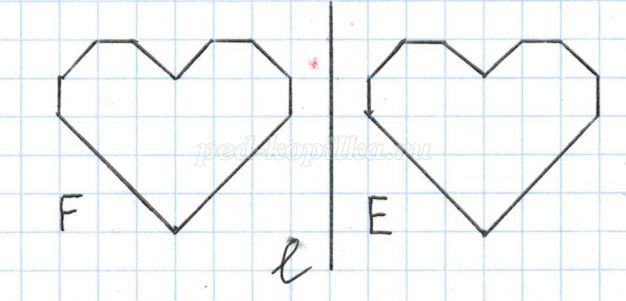
Осевая симметрия вокруг нас
Фигуры, обладающие осевой симметрией-Геометрические фигуры, симметричные относительно оси:
(угол, равнобедренный треугольник, прямоугольник, ромб, равносторонний треугольник, квадрат, окружность)
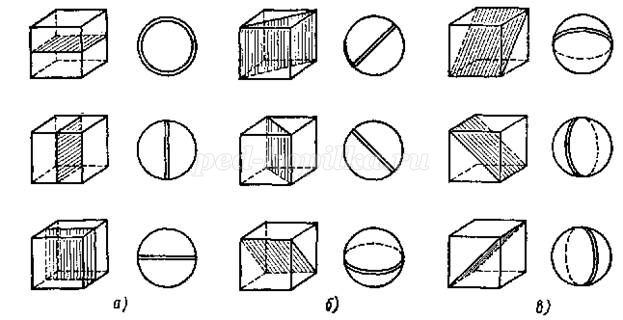
Объяснение новой темы
Используя перпендикулярность прямой и плоскости, введем важное понятие симметрии относительно плоскости, или зеркальной симметрии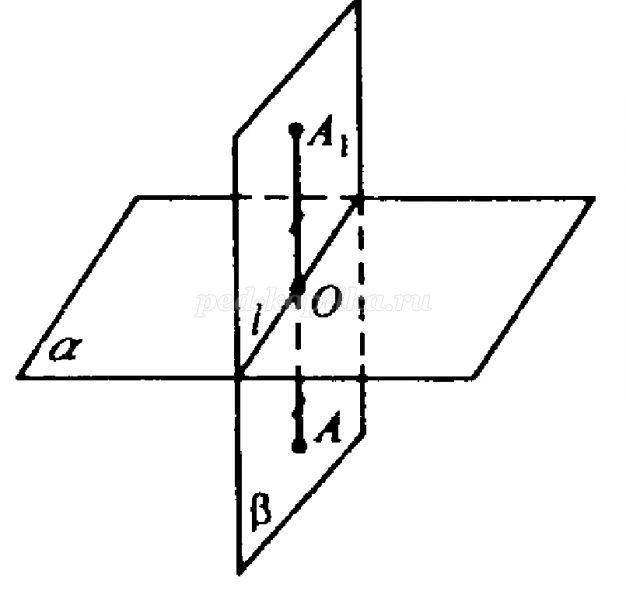
Роль плоскости симметрии выполняет зеркало, поэтому такая симметрия и получила название зеркальной.
При зеркальной симметрии каждая точка одной фигуры переходит в симметричную ей точку другой фигуры относительно данной плоскости.
Определение: Точки А и А1 называются симметричными относительно плоскости, если прямая АА1 перпендикулярна плоскости в точке О и ОМ=ОМ1
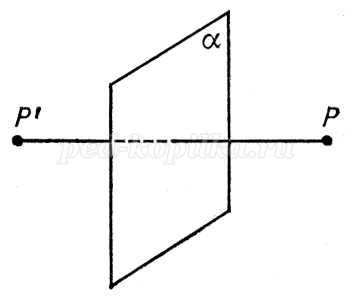
Пусть у нас есть фигура А и плоскость. Если построить точки, симметричные точкам фигуры А относительно плоскости, мы получим фигуру А1, симметричную фигуре А относительно плоскости.
Определение: Симметрией относительно плоскости называется преобразование пространства, при котором все точки переходят в симметричные им относительно этой плоскости точки.
Говорят, что точка А при симметрии относительно плоскости перешла в точку А1.
Перечислим свойства симметрии относительно плоскости:
1.Зеркальная симметрия является геометрическим преобразованием.
2.При зеркальной симметрии расстояния между соответствующими точками фигур сохраняются.
3.Симметрия относительно плоскости является изометрией.
4.Каждая фигура при зеркальной симметрии переходит в равную ей фигуру.
Мир зеркальной симметрии. Симметрия в природе и на практике.
Отражение в воде – хороший пример зеркальной симметрии в природе. Мы любуемся пейзажами художников, удачными снимками. Горы красиво отражаются на поверхности озера, придавая снимку законченность. Поверхность озера играет роль зеркала, и воспроизводит отражение с геометрической точностью. Поверхность воды есть плоскость симметрии...
Примерами зеркальных отражений одна другой могут служить рука человека. Эффект зеркальной симметрии часто используют на практике. Так, в обувных магазинах на витрину иногда ставят только одну туфлю. Туфля отражается в зеркале, и зрительно нам кажется , будто мы видим пару туфель.
Герман Вейль сказал: «Симметрия является той идеей, по средствам которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство». Герман Вейль – это немецкий математик. Его деятельность приходится на I половину XX века.
Именно он сформулировал определение симметрии, установил, по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае
Действительно, симметричность приятна глазу.
Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, - всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии.
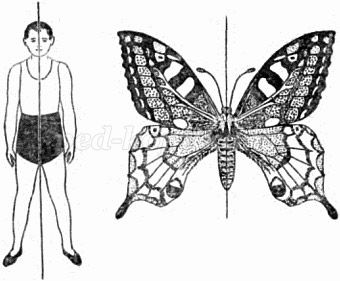
В окружающем нас мире много фигур (объектов), имеющих плоскость симметрии. Плоскости симметрии имеют многие инструменты (рубанки, молотки, лопаты). Симметричны относительно плоскости трубы, подшипники, автомобили
а) Архитектурные произведения отражают исключительные свойства симметрии. Большинство зданий зеркально симметричны
б) Узоры на коврах тоже симметричны
в) Симметрия широко встречается в прикладном искусстве. Орнаменты, карнизы имеют в своей основе периодически повторяющийся узор.
г) в быту.
Симметрия в природе

Вопрос: Назовите фигуры или предметы, симметричные относительно плоскости у нас в кабинете.
Давайте послушаем выступление на данную тему (выступление заранее подготовленного обучающегося)
IV. Закрепление знаний.
1.Как вы думаете, где применяется симметрия у вас в профессии? Рассмотрим на примерах.
2.Решение задач.
а) Являются ли точки симметричными относительно данной точки
б) Какие из следующих букв имеют центр симметрии
в) Какие из следующих букв имеют ось симметрии:
г) Являются ли данные точки симметричными относительно оси?
3. Решение ребусов для логического мышления
4.Выполнение тестовой работы в 2 вариантах.
5. Задача по учебнику А.В.Погорелова «Геометрия» №16,17,18
V. Домашняя работа.
1.Ответить на вопросы по учебнику В.А.Гусев «Математика» п.22.2-22.3 стр.261
2.Подготовить презентацию на тему:«Симметрия в природе»
VI. Рефлексия
Что мы с вами проходили на этом уроке?
Перечислите виды симметрий в пространстве?
Зачем нужно знать человеку о симметрии?
VII. Заключение урока, выставление оценок.
Приложения:
ВыступлениеОсновные принципы строения человеческого организма были заложены миллиарды лет назад, когда еще появились первые клетки и генетический код. Одним из признаков, которые перешли к нам является симметричность человеческого организма. Знаменитый врач Трифонов, когда изучал причины появления разных болезней, пришел к выводу: оказывается, что причинами наших болезней являются не только вирусы. Изменения генетической конструкции человеческого тела также вызывают разные болезни.
Оказывается, что симметричные животные живут дольше, чем несимметричные. Значит,симметрия это еще и признак здоровья.
Рекомендуем посмотреть:
 Урок математики по теме Диаграммы в 6 классе
Урок математики по теме Диаграммы в 6 классе
 Игра "Поле чудес" по математике для учащихся 5-6 классов коррекционных школ VIII вида
Игра "Поле чудес" по математике для учащихся 5-6 классов коррекционных школ VIII вида
 Внеклассное мероприятие по математике для учащихся коррекционных школ VIII вида
Внеклассное мероприятие по математике для учащихся коррекционных школ VIII вида
 Конспект урока математики в 5 классе «Путешествие в страну Математики»
Конспект урока математики в 5 классе «Путешествие в страну Математики»
Похожие статьи:
Игра как средство интерактивного обучения по предмету Математика
Конспект урока математики в 6 классе по теме: Умножение и деление обыкновенных дробей
Внеклассное мероприятие по математике для учащихся 7-8 класса. Игра «Слабое звено»
Конспект урока математики 9 класс по теме: Арифметическая и геометрическая прогрессии
← Конспект урока геометрии 10 класс. Симметрия в пространстве | Конспект воспитательного часа к Международному дню инвалидов для студентов техникума →
|
|
Автор: Бурганова Лилия Фаритовна
Опубликовано: 3614 дня назад (31 января 2015)
Просмотров: 10546
Рубрика: Статьи и разработки
|
0 Голосов: 0 |
Нет комментариев. Ваш будет первым!



