Технологическая карта урока с презентацией "Начала теории вероятностей", 8 класс
Начала теории вероятностей. Урок-исследование с презентацией и тетрадью на печатной основе
Автор: Красина Елена Михайловна, учитель математики МБОУ СОШ Чехов – 3 с углубленным изучением отдельных предметов.Описание: урок открытия нового знания предназначен для учителей математики, работающих в 7-8 классах. Это первое занятие в курсе «Теория вероятностей». Разработка даст возможность учителю использовать исторический материал, интересные примеры из кинематографа и окружающей жизни, а также эксперимент для развития познавательного интереса к новому разделу математики и формирования положительной мотивации учения.
Цель: рассмотреть основные понятия и формулу для вычисления вероятности случайных событий.
Задачи:
Образовательные:
- классифицировать события и сформулировать определения каждого вида;
- сформулировать классическое определение вероятности;
- составить алгоритм для вычисления вероятности случайного события, научиться применять данный алгоритм для решения задач.
Развивающие:
- создать условия для развития навыков самостоятельной работы, интеллектуальных качеств, умения анализировать, обобщать, выделять главное.
Воспитательные:
- создать условия для развития познавательного интереса к предмету и уверенности в своих силах;
- формировать положительную мотивацию учения.
Планируемые результаты:
Предметные:
- знать классификацию событий и определения;
- знать классическое определение вероятности и алгоритм нахождения вероятности случайного события;
- уметь определить вид события, находить вероятность случайного события по алгоритму.
Личностные:
- уметь слушать и вступать в диалог;
- участвовать в коллективном обсуждении проблем;
- проводить эксперимент и интерпретировать его результаты.
Метапредметные:
- уметь ставить перед собой цель;
- определять задачи;
- планировать последовательность действий;
- анализировать итоги деятельности и вносить коррективы;
- осуществлять самооценку и самоконтроль.
Образовательная технология: Технология деятельного метода.
Оборудование к занятию: интерактивная доска, презентация, тетрадь на печатной основе (распечатать на каждого ученика, обратить внимание, что необходимо 4 разных варианта первой страницы для получения на этапе актуализации различных ключевых слов), игральные кубики для эксперимента.
Дополнительные источники: в работе использованы высказывания Роберта Брингхерста, Готфрида Вильгельма Лейбница, видео фрагмент мультипликационного фильма "12 месяцев", фрагмент программы "Новости", песня «По теории вероятности» в исполнении Вадима Мулермана, музыка Игоря Крутого.
Ход урока:
I. Организационный момент. Мотивация к учебной деятельности.Учитель: О математике существует много различных высказываний. Но высказывание, которое мне близко по духу следующее:
«Математика существует не для того, чтобы навязывать кому-либо тяжелую работу. Наоборот, она существует только для ...» Роберт Брингхерст
В конце высказывания пропущено слово. Как бы вы закончили фразу?
Ученик: Радости, удовольствия.
Учитель: Вы получаете удовольствие от уроков математики? Когда это происходит?
Ученик: Когда удается решить сложную задачу, когда разобрался в новой теме. Удовольствие, что узнал для себя что-то новое и важное.
Учитель: Мы закончили предыдущую тему и написали контрольную работу. Что предстоит нам сегодня?
Ученик: Урок открытия новых знаний.
Учитель: Я надеюсь, что сегодня мы будем «поглощать знания» с удовольствием.
II. Актуализация опорных знаний учащихся, формирование темы урока, постановка цели.
Учитель: Что необходимо сделать перед тем как мы обратимся к новой теме?
Ученик: Повторить те знания, которые нам потребуются сегодня для открытия новых знаний.
Учитель: Для работы будем использовать фрагмент тетради на печатной основе, которую я для вас приготовила.
Откройте тетрадь, и выполните задание в разделе актуализации. В результате получится ключевое слово. Тех, кто составит слова первыми, я попрошу выйти и прикрепить их на доску.
Пример заданий для получения ключевого слова «Вероятность»

Сообщение темы урока и цели:
Учитель: Мы получили с вами основные понятия неизвестного вам еще раздела математики. Но может быть, кто-то слышал о нем?
Ученик: «Теория вероятностей»
Учитель: Что изучает теория вероятностей? Где мы можем найти ответ на этот вопрос?
Ученик: Например, в учебнике, в интернете, в теоретическом блоке тетради на печатной основе.
Теория вероятностей – математическая наука, изучающая закономерности массовых случайных событий.
Учитель: Дополните свой конспект недостающими словами.

Ученик: Рассматриваются основные определения, понятия, обозначения и т. д.
Учитель: Сформулируем тему и цель урока, опираясь на то, что это первый урок в теме.
Ученик: Тема: «Начала теории вероятностей». Цель: рассмотреть основные понятия и классическое определение вероятности.
III. Изучение нового материала
1. Историческая справка
Учитель: Обратимся к исторической справке (просмотр сюжета о зарождении «Теории вероятностей»).
2. Классификация видов событий
Учитель: В основе теории вероятностей лежит такое понятие, как событие.
Сейчас я проведу испытание с кубиком и произойдет событие (бросается кубик и смотрим, что выпало).
Обратите внимание, что событие обозначается большой латинской буквой. В фигурных скобках записывается его исход, то есть результат испытания.
А = {выпадение четного числа}
Что я должна записать в строку события В? Произведите свое испытание, подбросьте кубик и запишите событие, которое произошло - это событие С.


Ученик: Два. Достоверное и случайное.
Учитель: Внимание на экран, перед вами ряд событий. Нам надо распределить их по известным видам.
Ученики распределяют события по видам (достоверные и случайные).
Учитель: Два события мы были вынуждены пропустить. Почему?
Ученик: Мы не смогли эти события отнести ни к достоверным, ни к случайным.
Учитель: Значит наша классификация неполная. Предложите для этих событий название.
Ученик: Нереальные, не происходящие, несуществующие, невозможные.
Учитель: Дополните ваш опорный конспект в разделе «Виды событий».
Ученик:
1. Событие, которое обязательно наступит, называется достоверным.
2. Событие, которое никогда не наступит, называется невозможным.
3. Событие, которое может, как наступить, так и не наступить, называется случайным.
4. Любой результат испытания называется исход.

Назовите мне события, которые вы увидели в данном фрагменте.
Учащиеся: После 31 наступит 32 декабря и т. д.; в декабре распустятся подснежники.
Учитель: Как бы вы могли назвать данные события?
Ученики: Невозможные.
Учитель: Может у кого-то есть иное мнение? Я предлагаю посмотреть другой сюжет. Это новости 1 канала о событие, которое произошло в 2012 году в Белграде. Какой же можно сделать вывод из того, что мы увидели?
Ученики: Мы ошиблись по поводу второго события. Так как в реальной жизни такое событие произошло, то его уже нельзя назвать невозможным. Это случайное событие.
Учитель: Недавно, по историческим меркам, подарить девушке букетик подснежников было проявлением внимания, символом весны. Сегодня эти весенние цветы занесены в Красную книгу, как исчезающий вид. И такой подарок - это преступление против природы. Если мы не будем бережно относиться к первоцветам, то, возможно, ваши дети на уроке математики назовут такое событие, как «весной появились подснежники» уже невозможным. Ежегодно, 19 апреля, во многих странах мира отмечают красивый весенний праздник, уже ставший традиционным, - «День подснежника».

Ученики: Это редкое явление, и мы о нем не знали. Нам может не хватит знаний о том, что происходит в мире.
Учитель: «Редкое событие», «часто встречающееся», «иногда можно встретить» - это может являть с точки зрения математики возможностью произвести сравнительную оценку? Что мы можем сравнить, используя математический аппарат?
Ученик: Мы можем сравнить числа.
Учитель: Долю успеха того или иного события стали называть «вероятностью». А как мы знаем долю можно выразить числом. Хотите узнать, как это сделали великие математики прошлого?
3. Проведение эксперимента
Учитель: Предлагаю вам вернуться на несколько столетий назад и повторить их эксперимент. Вспомните исторический видео очерк. Какая игра подтолкнула ученых к исследованию?
Ученики: Игра в кости.
Учитель: Аналогом кости может служить игральный кубик. В детских играх вы не раз с ним встречались. Сегодня мы используем его в экспериментальной работе.
Эксперимент с игральным кубиком. Работа в парах.
1 ряд проводит 1 эксперимент, 2 ряд – 2 эксперимент и 3 ряд – 3 эксперимент. План работы на экране презентации и в тетради на печатной основе. Закончив эксперимент запишите ваш результат на доске, там, где записан номер вашего ряда.
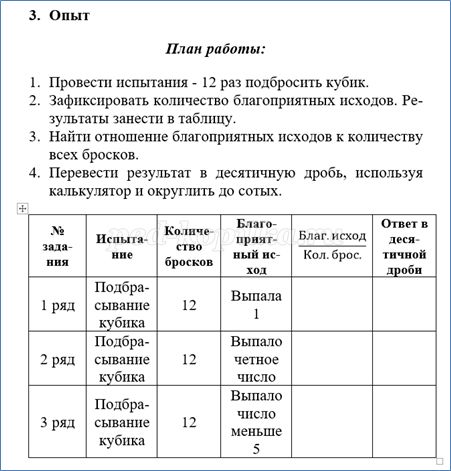
Ученик: Найдем отношение 2048 к 4040. После округления получили 0,5. Следовательно, частота события «выпал герб» в данном эксперименте равна 0,5.
Учитель: Английский математик Карл Пирсон в начале двадцатого столетия провел такой же эксперимент. Он подбрасывал монету 24000 раз. Пирсон считал сколько раз выпадет решка. В ходе эксперимента он установил, что она выпала в 12012 случаях. Опираясь на то, что мы уже проанализировали результаты эксперимента Жоржа Бюфона сделайте вывод.
Ученик: Найдем отношение 1202 к 2400, округлим. Следовательно, частота события «выпадения решки» в данном эксперименте равна 0,5.

Ученик: Мы провели малое количество экспериментов.
Учитель: Следовательно, чем больше испытаний, тем ближе вероятность, полученная опытным путем к действительности.
Проблемные вопросы: Удобен ли экспериментальный метод для вычисления вероятности события? Почему? Какое знание могло бы нам помочь?
Ученик: Неудобно, так как требует большого количества испытаний и много времени. Если была бы формула или алгоритм, то это был бы оптимальный вариант для нахождения вероятности.
4. Классическое определение вероятности
Учитель: Работаем в тетради на печатной основе. Опираясь на определение запишем формулу и составим алгоритм.

5.Алгоритм вычисления вероятности.
Шаг 1. Определю число n =… - количество всех возможных исходов.
Шаг 2. Определю число m =… - количество благоприятных исходов.
Шаг 3. Найду отношение: Р(А) = m/n

Вероятность невозможного события Р(А) = 0
Вероятность достоверного события Р(В) = 1
Вероятность случайного события Р(С)принадлежит промежутку (0;1).
IV. Закрепление
1. Фронтальная работа: решение экспериментального задания аналитически, работа в тетради на печатной основе.
Учитель: Экспериментально вам не удалось прийти к единому мнению. Давайте решим проблему аналитически.
Объясняет 1 ряд:
Шаг 1. n = 6
Шаг 2. m = 1
Шаг 3.Р(А) = 1/6
Объясняет 2 ряд:
Шаг 1. n = 6
Шаг 2. m = 3
Шаг 3. Р(А) = 0,5
Объясняет 3 ряд:
Шаг 1. n = 6
Шаг 2. m = 4
Шаг 3. Р(А) = 2/3
Учитель: Решим задачи с использованием алгоритма.
Задача 1: На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет. (Ответ: 0,88)
Задача 2: На тарелке лежат пирожки 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. (Ответ: 0,25)
2. Парная работа: решаем по вариантам с комментированием вслух. Самопроверка по образцу.
Учитель: 1 вариант решает, оформляет и рассказывает 2 варианту.
Задача: В фирме такси в данный момент свободно 9 черных, 4 желтых и 7 зеленых машин. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. (Ответ: 0,2)
Учитель: 2 вариант решает, оформляет и рассказывает 1 варианту
Задача: В среднем из 100 карманных фонариков, поступивших в продажу, восемь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен. (Ответ: 0,92)
V. Рефлексия
1) Что вы нового узнали сегодня на уроке?
2) Какие этапы были самыми интересными?
3) Чем запомнился сегодняшний урок?
4) Что вызвало затруднение?
Учитель: Обратите внимание, что у вас на тетради есть стикер. Я попрошу вас оценить свою заинтересованность в данной теме. Вы готовы изучать её только в рамках обязательного уровня? Проанализируйте, может вы, готовы решать задачи по теории вероятности на повышенном уровне, чтобы успешно справляться с ними на ЕГЭ, на олимпиаде? Или же вы хотели бы заниматься исследовательской работой по данным вопросам (теория вероятностей и статистика – это перспективные направления в разных областях науки)? Прежде чем покинуть кабинет прикрепите свой стикер на ось математического удовлетворения на выбранный промежуток. Это поможет понять, какие у вас запросы в данной теме и подобрать соответствующий материал.
VI. Домашнее задание
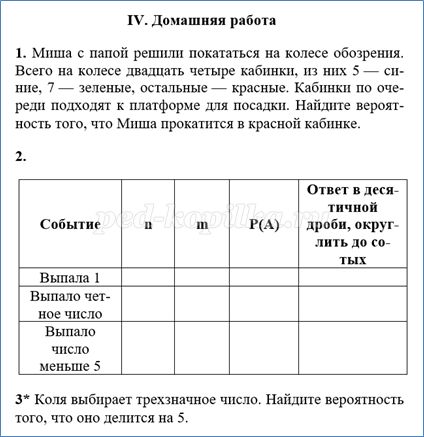
1. Задачи в тетради с печатной основой.
Заключение: Как это не странно, но в Древней Греции музыка входила в триаду наук, а не искусства. «Музыка есть таинственная арифметика души», - говорил Лейбниц. Интересные, ассоциативные научные понятия и теории находят отражения в песнях и творчестве. Я предлагаю вам послушать, какие ассоциации возникли у автора песни «По теории вероятности» в исполнении Вадима Мулермана.
Скачать Технологическая карта урока "Начала теории вероятностей"
Презентация на тему: Начала теории вероятностей
Рекомендуем посмотреть:
 Конспект урока алгебры по теме "Квадратные уравнения" с использованием интерактивного учебного пособ
Конспект урока алгебры по теме "Квадратные уравнения" с использованием интерактивного учебного пособ
 Многоуровненвая система учебно - тренеровочных задач по теме: Дробно-рациональные уравнения, 8 клас
Многоуровненвая система учебно - тренеровочных задач по теме: Дробно-рациональные уравнения, 8 клас
 Конспект урока алгебры, 8 класс. Арифметический квадратный корень
Конспект урока алгебры, 8 класс. Арифметический квадратный корень
 Зачетная работа по теории вероятностей и математической статистике для студентов 2 курса
Зачетная работа по теории вероятностей и математической статистике для студентов 2 курса
Похожие статьи:
Конспект урока по алгебре в 8 классе. Решение квадратных уравнений
Открытый урок по алгебре в 8 классе «Решение квадратных уравнений по формуле»
Урок алгебры в 8 классе. Тема урока: «Решение задач с помощью рациональных уравнений»
Участник №16 профессионального конкурса для педагогов на лучшую методическую разработку с 20 июня по 20 сентября 2019 года
|
|
Автор: Елена Михайловна Красина
Опубликовано: 2073 дня назад (15 июля 2019)
Просмотров: 5299
Рубрика: Без рубрики
|
+5↑ Голосов: 5 |
| # 16 июля 2019 в 11:14 +1 |
| # 16 июля 2019 в 14:29 +1 | ||
|
| # 20 июля 2019 в 08:49 +1 |
| # 26 июля 2019 в 01:38 +1 |
| Добрый день! Я подробно ознакомилась с предложенными Вами материалами. Мне как молодому специалисту очень важна структура. В Вашей работе все максимально подробно и последовательно изложено. Также хочу отметить техническое сопровождение, разнообразные формы. Ваша работа вдохновляет. Желаю Вам успехов и советую создать свой личный сайт с Вашими работами. Очень бы хотелось с ним ознакомиться. Отдаю Вам свой голос! |
| # 5 сентября 2019 в 21:43 +1 | ||
|



