Урок по математике и географии в 6 классе на тему: Масштаб

Провели: Мухина Е.А., Емельянова Н.А., учителя математики и географии , МБОУ "СОШ №31", г.Симферополь, Республика Крым

Цель урока:
Познакомить учащихся с видами масштаба - численным, линейным, именованным. Научить детей пользоваться этими видами масштаба, решать соответствующие задачи, дать учащимся математическое и географическое понятие масштаба; углубление межпредметных связей.
Оборудование:
мультимедийная доска, компьютер, линейки, циркули, карандаши, планы местности.

1.Организационный этап.
2.Проверка домашнего задания.
3.Актуализация опорных знаний учащихся.
4.Формулирование темы, цели и задач урока.Мотивация учебной деятельности.
5.Восприятие и осознание нового материала.

Географ задает ученикам вопросы. Получив ответы , анализирует их правильность.
-- Какими единицами длины и какими инструментами измеряют расстояния на местности?
-- Метрами и километрами; рулеткой, счетчиком, спидометром и др.
--Как вы понимаете выражения «расстояние между оазисами равно четырехнедельному переходу на верблюдах», «расстояние от Москвы до Владивостока составляет десятидневное путешествие на поезде»? Чему будут равны эти расстояния?
--На этот вопрос можно ответить приблизительно, если знать скорость.
--Как переводятся термины «географии» и «геометрия»?
--«Землеописание» и «землемерие».
--Какая связь между этими понятиями?
--Геометрия развивалась первоначально как метод измерения на земной поверхности. География-это изучение и описание Земли.
Далее учитель объясняет, что для того, чтобы составить план или карту, необходимо проводить точные измерения расстояний между географическими объектами, а чтобы их нанести на бумагу, эти расстояния нужно уменьшить в определенное количество раз.

Математик.
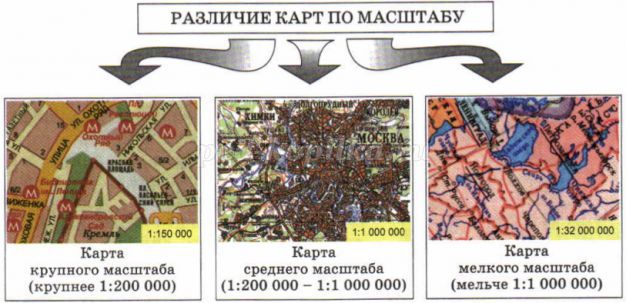
--Например, расстояние 1000 м изображают на карте отрезком в 1 см. Так как 1000 м=100 000 см, то каждый отрезок на карте в 100 000 раз меньше соответствующего отрезка на местности. Это записывают в виде дроби 1:100000.
Запишите определение в тетрадь.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
В географии такой масштаб называют численным.
По-другому это формулировку можно дать следующим образом:
Масштабом называется дробь, у которой числитель - единица, а знаменатель-число, показывающее, во сколько раз расстояние на плане меньше, чем на местности.
В качестве знака деления применяют двоеточие, а не дробную черту.
Задача 1. Длина отрезка на карте 3 см. Найти длину соответствующего отрезка на местности, если масштаб карты 1:1 000 000.
Решение. Обозначим длину отрезка на местности ( в см) буквой х и найдем отношение длины отрезка на карте к длине отрезка на местности.
3 см : х =1 : 1 000 000. Решив уравнение, получим х =3 см. Тогда
1 000 000 = 3 000 000 см. Но 3 000 000 см = 30 000 м = 30 км.
Ответ: 30 км.

Географ .
--Чтобы по дине линии на плане или карте удобно было узнавать расстояние на местности, у численного масштаба пишут пояснения: в 1 см – 10 км, в 1 см – 100 м, в 1 см – 10 м и т.д. То есть сантиметры переводят в метры и километры.
Такой масштаб называют именованным.
Задача 2. Определите длину школьного сада по плану, если на плане его длина 4 см, а масштаб плана в 1 см – 10 м.
Решение. 4х10 м = 40 м, то есть 4 см – это на местности 40 м.
В жизни часто встречаются случаи, когда величину предмета на чертеже или рисунке нужно не уменьшить, а увеличить. В учебниках географии можно видеть фотографии и рисунки мельчайших растений и животных, живущих в морях и океанах. Многие из них видны только под микроскопом. Чтобы их изобразить, пришлось их сильно увеличить. На технических чертежах мелкие детали механизмов показывают увеличенными. В таких случаях единица служит не числителем, а знаменателем численного масштаба: 500 : 1, 10 : 1, 2 : 1.

6.Закрепление изученного материала.

Математик предлагает ученикам решить задачи.
Задача 3. Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1 : 100 000?
Решение. Обозначим длину ( в км) отрезка на карте буквой х и составим пропорцию: х : 4,5 = 1 : 100 000. Тогда х * 100 000 = 4,5 * 1, отсюда
х = 4,5 : 100 000. Получаем, что х = 0,000045.
Но 0,000045 км = 0,045 м = 4,5 см.
Ответ: длина отрезка на карте 4,5 см.
По такому образцу можно решить и ряд других задач.
1)Определите расстояние по карте от устья ручья Стача до устья ручья, протекающего близ дер. Демидово. Масштаб карты 1 : 25 000.
2)Расстояние между городами А и В на карте равно 8,5 см. Найдите расстояние между городами на местности, если масштаб карты 1 : 1 000 000.
3)Длина железной дороги Москва – Санкт - Петербуг приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб
1 : 10 000 000.
4)Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной страницы тетради это расстояние при масштабе одна десятимиллионная?
5)На рисунке дан план квартиры в масштабе 1 : 100. Определите по плану, какие размеры имеют кухня, ванная и комнаты и какова их площадь в действительности.
6)Отрезку на карте длиной 3,6 см соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на это карте расстояние между ними 12,6 см?
7)Длина железнодорожной магистрали 6140 км. Какой длины получится линия, изображающая магистраль на карте, сделанной в масштабе: а) 1 : 10 000 000; б) 1 : 2 000 000.
8)Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на карте длина отрезка, изображающего отрезок 10 км? Какой отрезок на местности изображает отрезок на карте длиной 1,8 см?
9)Длина детали на чертеже, сделанном в масштабе 1 : 5, равна 7,2 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 1 : 3? В масштабе 2 : 1?

7.Дальнейшее восприятие и осознание нового материала.

Географ.
-- Есть ещё один вид масштаба – линейный. Он позволяет измерять расстояние на плане и карте, не прибегая к вычислениям.
Он представляет собой прямую линию, разделенную на равные части. У каждого деления линии подписывают соответствующие ему расстояния на местности. Одно такое деление откладывают влево от нуля, его делят на более мелкие части (обычно 5 или 10).
Чтобы пользоваться линейным масштабом, нужно определить, чему равны большое и маленькое деления. Измеряемый отрезок нужно отложить на линейном масштабе циркулем от нуля вправо ( на рисунке – положение 1). Правая ножка циркуля оказывается при этом обычно где-то в пределах большого отрезка, а не на его конце. Сдвинем циркуль немного влево (положение 2) , чтобы правая ножка пришлась на конец большого отрезка. При этом мы сможем получить длину отрезка как сумму больших отрезков вправо от нуля и маленьких отрезков влево от него.
В заключение предлагаются два-три упражнения на определение расстояния с помощью линейного масштаба.


8.Домашнее задание.

9.Подведение итогов урока. Выставление оценок. Заключительное слово.
10.Рефлексия.
1. Какие цели к уроку ставили?
2. Достигли ли мы их?
3. Как Вы оцениваете свою работу на уроке?

Спасибо за внимание!!!

Рекомендуем посмотреть:

Конспект урока математики для 6 класса коррекционной школы VIII вида по теме: Скорость. Время. Расст Конспект урока по географии в 6 классе «Реки» Математический калейдоскоп. Математика 6 класс Внеклассное мероприятие по математике для 6 класса. Конспект

Похожие статьи:

Внеклассное мероприятие по математике для 5-6 классов

Рабочая программа по математике 6 класс Виленкин

Технологическая карта урока математики, реализующего формирование УУД

Открытый урок по математики в 6 классе

Внеклассное мероприятие по математике, 6-7 класс