Олимпиада по математике для 1-4 класса
Олимпиада в начальной школе по математике
Учитель: Петрюк Елена Владимировна - Филиал МОУ СОШ № 17 – СОШ № 3 г. Карталы, Челябинская обл.
Описание материала: Проведение олимпиад в начальной школе имеет большое воспитательное и обучающее значение. Олимпиады позволяют ученику познать себя, дают возможность в большой степени почувствовать в себе уверенность, служат развитию творческой инициативы ребёнка.
Олимпиадные задания с 1 по 4 классы.
Отличительной особенностью школы является обязательное участие полных команд в интеллектуальных соревнованиях по общеобразовательным предметам школьного, районного, городского уровней.
Основными целями и задачами для организатора проведение конкурсов знаний в этой связи являются:
• создание оптимальных условий для выявления одарённых и талантливых детей, их дальнейшего интеллектуального развития и профессиональной ориентации;
• пропаганда научных знаний и развитие у школьников интереса к научной деятельности;
• обязательный сравнительный анализ результатов участия в конкурсах, смотрах, олимпиадах на разных уровнях;
• постоянная учебная работа с конкурсными заданиями, решение олимпиадных задач в процессе очной и заочной подготовки школьных команд;
• моральное и материальное стимулирование педагогов и учащихся к достижению высоких результатов выполнения заданий повышенной сложности.
Форма проведения интеллектуальных соревнований могут быть самыми разными: смотры знаний, интеллектуальные марафоны, КВН, викторины, конкурсы знатоков, «Что? Где? Когда?» и т. д. Но наиболее эффективной формой работы является олимпиада.
Проведение олимпиад в начальной школе имеет большое воспитательное и обучающее значение. Олимпиады позволяют ученику познать себя, дают возможность в большой степени почувствовать в себе уверенность, служат развитию творческой инициативы ребёнка.
Я предлагаю вам задания по математике, чтобы подготовить детей к олимпиаде
1 класс
I. «Поспевай – не зевай»
Учитель читает вопрос, дети должны быстро дать ответ, не поднимая руки.
1. К какому числу надо прибавить 2, чтобы получилось 10? (8)
2. Что в хлебе родится, а есть не годится? (Василёк0
3. Тише едешь - … (Дальше будешь)
4. Сколько звуков в слове «юла»? (4)
5. Паук – насекомое? (Нет)
6. Шестой день недели. (Суббота)
7. Вьют или нет наши перелётные птицы гнёзда на юге? (нет)
8. Личинка бабочки (Гусениц
9.Долговяз в землю увяз. (Дождь)
10.Сколько звуков в слове «яма» (4)
11. В каком слове 100 «л»? (Стол)
12. Чёрная малина? (Ежевика)
II. Решение задач
1. Как число 10 можно записать пятью одинаковыми числами, соединив их знаками действия?
(Ответ: 2+2+2+2+2=10)
2. Витя поднимался по лестнице. Он прошёл 3 ступеньки, а затем стал шагать через одну. Запиши все номера ступенек, на которые он наступал, если на лестнице было 12 ступенек.
(Ответ: 1,2,3,5,7,8,10)
3. Если Дима ростом не выше Олега, то каким он может быть ростом по сравнению с Олегом?
(Ответ: Дима может быть ниже Олега или иметь такой же рост, что и Олег.)
4. Скольки способами могут сесть на скамейку в один ряд три подруги Аня, Маша и Наташа?
(Ответ: 6 способами.)
III. Игра
Я задумала двузначное число, вычел из него 1 и получил однозначное число. Какое число я задумал?
(Ответ: единственное двузначное число, которое на 1 больше однозначного числа – это 10. Получаем: 10-1=9.)
2 класс
1. Геологи нашли 7 камней, массы которых 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг, 7 кг. Эти камни разложили в 4 рюкзака так, что в каждом рюкзаке масса камней была одинаковая. Как это сделать?
(Ответ: найдём общую массу всех 7 камней: 1+2+3+4+5+6+7=28 кг. Тогда в каждом рюкзаке будет по 28:4=7 кг камней. В рюкзаке камни можно разложить так: камень 7 кг; 6 кг и 1 кг; камни 4 кг и 3 кг.)
2. Написано 99 чисел: 1, 2, 3…98, 99. Сколько раз в записи встречается цифра 5?
(Ответ: в записи ряда чисел от 1 до 99 цифра 5 встречается 20 раз.)
3. Четыре человека обменялись рукопожатиями. Сколько всего было рукопожатий?
(Ответ: 4 человека обменялись шестью рукопожатиями.)
4. 3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 12 кур за 12 дней, если они будут нести такое же количество яиц за один и тот же промежуток времени?
(Ответ: 12:3=4 (раз), 12*4=48 (яиц), таким образом 48)
5. Термометр показывает 5 градусов мороза. Сколько градусов покажут 2 таких термометра?
(Ответ: 5 градусов)
6. Поставь двух мальчиков так, чтобы Олег стоял сзади Петра, а Пётр стоял сзади Олега.
(Ответ: надо поставить мальчиков спиной друг к другу.)
7. Раздели квадрат на 4 равные части, чтобы из них можно было составить 2 квадрата.
Ответ:
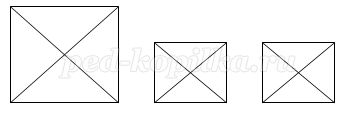 8. Положи 3 палочки так, чтобы получилось 3 острых угла и 2 тупых угла
8. Положи 3 палочки так, чтобы получилось 3 острых угла и 2 тупых угла
Ответ: возможно несколько случаев
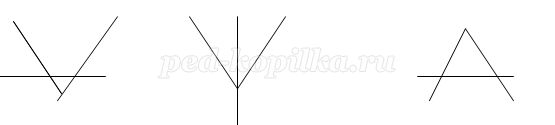
3 класс
1. Улитка каждый день вползает по стене на 5 м вверх и ночью спускается на 3 м вниз. На какой день она, начав от земли, достигнет крыши дома, высота которого 15 м?
(Ответ: на шестой день)
2. Какую часть года составят два месяца?
(Ответ: шестую часть)
3.Чтобы найти пиратский клад, надо пройти от старого дуба 12 шагов на север, потом 5 шагов – на юг, потом ещё 4 шага – на север и ещё 11 шагов – на юг. Узнай, где зарыт пиратский клад?
(Ответ: клад зарыт под дубом)
4. Подчеркни лишнее число: 19, 17, 12, 15, 21
(Ответ: 12 – оно чётное, или 21 – у него два десятка)
5. Продолжи ряд: 5, 9, 17, 29…., …,…,
(Ответ: 5+4=9, 9+8=17, 17+12=-29, 29+16=45,65,89…)
6. Число 12 больше задуманного числа в 3 раза. Чему равно задуманное число?
(Ответ:4)
7. Вова покрасил каждую грань кубика разными красками. Сколько красок потребовалось?
(Ответ: 6 красок)
8. В колесе 12 спиц. Сколько промежутков между спицами?
(Овеет: 12 промежутков)
4 класс
1. Раскрасьте все 16 клеток квадрата 4х4 красным, синим, зелёным и жёлтым цветами так, чтобы в каждой строке и в каждом столбце цвета не повторялись.
Ответ:
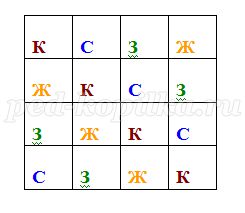 2. В семье трое детей: два мальчика и девочка. Их имена начинаются с букв А, В, Г. среди А и В есть начальная буква имени одного мальчика. Среди В и Г есть начальная буква имени одного мальчика с какой буквы начинается имя девочки?
2. В семье трое детей: два мальчика и девочка. Их имена начинаются с букв А, В, Г. среди А и В есть начальная буква имени одного мальчика. Среди В и Г есть начальная буква имени одного мальчика с какой буквы начинается имя девочки?
(Овеет: имя девочки начинается на В.)
3. Вол и заяц соревновались в беге. Каждый шаг зайца был в 2 раза короче волчьего, но шаги заяц делал в 3 раза чаще, чем волк. Кто победил в соревновании?
(Ответ: Выразим скорость волка и зайца в заячьих шагах: 1 шаг волка=2 шагам зайца, но так как шаги заяц делал в 3 раза чаще, то в то время, как волк делал 2 заячьих шага, заяц делал три шага. Значит, заяц победил.)
4. Из книги выпало несколько листов. Первая страница выпавших листов имеет номер 213, а номер их последней страницы изображается теми же цифрами, но в ином порядке. Сколько листов выпало из книги?
(Ответ: 50 листов. 313-213=100, 100:2=50)
5. Подбери двузначное число, цифра единиц которого в 7 раз меньше самого числа
(Ответ: 35)
6. Между некоторыми цифрами 1 2 3 4 5 поставь знаки действий и скобки так, чтобы получилось 1.
(Ответ: (1+23):4-5=1)
7. Инопланетяне сообщили жителям Земли, что в системе их звезды есть три планеты А, Б, В. они живут на второй планете. Далее передача ухудшилась из-за помех, но было принято ещё два сообщения, которые, как установили учёные, оба неверные:
1) А – не третья от звезды планета;
2) Б – вторая планета.
На какой планете А, Б, или В живут инопланетяне?
(Ответ: Разумные существа живут на планете В)
8. Какой цифрой оканчивается произведение: 13*14*15*16*17?
(Ответ: произведение оканчивается цифрой 0)
 Школьная олимпиада по математике 4 класс
Школьная олимпиада по математике 4 класс
 Решение нестандартных задач по математике в начальной школе
Решение нестандартных задач по математике в начальной школе
 Решение нестандартных задач по математике в начальной школе. Движение гусеницы
Решение нестандартных задач по математике в начальной школе. Движение гусеницы
 Решение нестандартных задач в начальной школе. "Задачи на уравнивание"
Решение нестандартных задач в начальной школе. "Задачи на уравнивание"
Учитель: Петрюк Елена Владимировна - Филиал МОУ СОШ № 17 – СОШ № 3 г. Карталы, Челябинская обл.
Описание материала: Проведение олимпиад в начальной школе имеет большое воспитательное и обучающее значение. Олимпиады позволяют ученику познать себя, дают возможность в большой степени почувствовать в себе уверенность, служат развитию творческой инициативы ребёнка.
Олимпиадные задания с 1 по 4 классы.
Отличительной особенностью школы является обязательное участие полных команд в интеллектуальных соревнованиях по общеобразовательным предметам школьного, районного, городского уровней.
Основными целями и задачами для организатора проведение конкурсов знаний в этой связи являются:
• создание оптимальных условий для выявления одарённых и талантливых детей, их дальнейшего интеллектуального развития и профессиональной ориентации;
• пропаганда научных знаний и развитие у школьников интереса к научной деятельности;
• обязательный сравнительный анализ результатов участия в конкурсах, смотрах, олимпиадах на разных уровнях;
• постоянная учебная работа с конкурсными заданиями, решение олимпиадных задач в процессе очной и заочной подготовки школьных команд;
• моральное и материальное стимулирование педагогов и учащихся к достижению высоких результатов выполнения заданий повышенной сложности.
Форма проведения интеллектуальных соревнований могут быть самыми разными: смотры знаний, интеллектуальные марафоны, КВН, викторины, конкурсы знатоков, «Что? Где? Когда?» и т. д. Но наиболее эффективной формой работы является олимпиада.
Проведение олимпиад в начальной школе имеет большое воспитательное и обучающее значение. Олимпиады позволяют ученику познать себя, дают возможность в большой степени почувствовать в себе уверенность, служат развитию творческой инициативы ребёнка.
Я предлагаю вам задания по математике, чтобы подготовить детей к олимпиаде
1 класс
I. «Поспевай – не зевай»
Учитель читает вопрос, дети должны быстро дать ответ, не поднимая руки.
1. К какому числу надо прибавить 2, чтобы получилось 10? (8)
2. Что в хлебе родится, а есть не годится? (Василёк0
3. Тише едешь - … (Дальше будешь)
4. Сколько звуков в слове «юла»? (4)
5. Паук – насекомое? (Нет)
6. Шестой день недели. (Суббота)
7. Вьют или нет наши перелётные птицы гнёзда на юге? (нет)
8. Личинка бабочки (Гусениц
9.Долговяз в землю увяз. (Дождь)
10.Сколько звуков в слове «яма» (4)
11. В каком слове 100 «л»? (Стол)
12. Чёрная малина? (Ежевика)
II. Решение задач
1. Как число 10 можно записать пятью одинаковыми числами, соединив их знаками действия?
(Ответ: 2+2+2+2+2=10)
2. Витя поднимался по лестнице. Он прошёл 3 ступеньки, а затем стал шагать через одну. Запиши все номера ступенек, на которые он наступал, если на лестнице было 12 ступенек.
(Ответ: 1,2,3,5,7,8,10)
3. Если Дима ростом не выше Олега, то каким он может быть ростом по сравнению с Олегом?
(Ответ: Дима может быть ниже Олега или иметь такой же рост, что и Олег.)
4. Скольки способами могут сесть на скамейку в один ряд три подруги Аня, Маша и Наташа?
(Ответ: 6 способами.)
III. Игра
Я задумала двузначное число, вычел из него 1 и получил однозначное число. Какое число я задумал?
(Ответ: единственное двузначное число, которое на 1 больше однозначного числа – это 10. Получаем: 10-1=9.)
2 класс
1. Геологи нашли 7 камней, массы которых 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг, 7 кг. Эти камни разложили в 4 рюкзака так, что в каждом рюкзаке масса камней была одинаковая. Как это сделать?
(Ответ: найдём общую массу всех 7 камней: 1+2+3+4+5+6+7=28 кг. Тогда в каждом рюкзаке будет по 28:4=7 кг камней. В рюкзаке камни можно разложить так: камень 7 кг; 6 кг и 1 кг; камни 4 кг и 3 кг.)
2. Написано 99 чисел: 1, 2, 3…98, 99. Сколько раз в записи встречается цифра 5?
(Ответ: в записи ряда чисел от 1 до 99 цифра 5 встречается 20 раз.)
3. Четыре человека обменялись рукопожатиями. Сколько всего было рукопожатий?
(Ответ: 4 человека обменялись шестью рукопожатиями.)
4. 3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 12 кур за 12 дней, если они будут нести такое же количество яиц за один и тот же промежуток времени?
(Ответ: 12:3=4 (раз), 12*4=48 (яиц), таким образом 48)
5. Термометр показывает 5 градусов мороза. Сколько градусов покажут 2 таких термометра?
(Ответ: 5 градусов)
6. Поставь двух мальчиков так, чтобы Олег стоял сзади Петра, а Пётр стоял сзади Олега.
(Ответ: надо поставить мальчиков спиной друг к другу.)
7. Раздели квадрат на 4 равные части, чтобы из них можно было составить 2 квадрата.
Ответ:

Ответ: возможно несколько случаев

3 класс
1. Улитка каждый день вползает по стене на 5 м вверх и ночью спускается на 3 м вниз. На какой день она, начав от земли, достигнет крыши дома, высота которого 15 м?
(Ответ: на шестой день)
2. Какую часть года составят два месяца?
(Ответ: шестую часть)
3.Чтобы найти пиратский клад, надо пройти от старого дуба 12 шагов на север, потом 5 шагов – на юг, потом ещё 4 шага – на север и ещё 11 шагов – на юг. Узнай, где зарыт пиратский клад?
(Ответ: клад зарыт под дубом)
4. Подчеркни лишнее число: 19, 17, 12, 15, 21
(Ответ: 12 – оно чётное, или 21 – у него два десятка)
5. Продолжи ряд: 5, 9, 17, 29…., …,…,
(Ответ: 5+4=9, 9+8=17, 17+12=-29, 29+16=45,65,89…)
6. Число 12 больше задуманного числа в 3 раза. Чему равно задуманное число?
(Ответ:4)
7. Вова покрасил каждую грань кубика разными красками. Сколько красок потребовалось?
(Ответ: 6 красок)
8. В колесе 12 спиц. Сколько промежутков между спицами?
(Овеет: 12 промежутков)
4 класс
1. Раскрасьте все 16 клеток квадрата 4х4 красным, синим, зелёным и жёлтым цветами так, чтобы в каждой строке и в каждом столбце цвета не повторялись.
Ответ:

(Овеет: имя девочки начинается на В.)
3. Вол и заяц соревновались в беге. Каждый шаг зайца был в 2 раза короче волчьего, но шаги заяц делал в 3 раза чаще, чем волк. Кто победил в соревновании?
(Ответ: Выразим скорость волка и зайца в заячьих шагах: 1 шаг волка=2 шагам зайца, но так как шаги заяц делал в 3 раза чаще, то в то время, как волк делал 2 заячьих шага, заяц делал три шага. Значит, заяц победил.)
4. Из книги выпало несколько листов. Первая страница выпавших листов имеет номер 213, а номер их последней страницы изображается теми же цифрами, но в ином порядке. Сколько листов выпало из книги?
(Ответ: 50 листов. 313-213=100, 100:2=50)
5. Подбери двузначное число, цифра единиц которого в 7 раз меньше самого числа
(Ответ: 35)
6. Между некоторыми цифрами 1 2 3 4 5 поставь знаки действий и скобки так, чтобы получилось 1.
(Ответ: (1+23):4-5=1)
7. Инопланетяне сообщили жителям Земли, что в системе их звезды есть три планеты А, Б, В. они живут на второй планете. Далее передача ухудшилась из-за помех, но было принято ещё два сообщения, которые, как установили учёные, оба неверные:
1) А – не третья от звезды планета;
2) Б – вторая планета.
На какой планете А, Б, или В живут инопланетяне?
(Ответ: Разумные существа живут на планете В)
8. Какой цифрой оканчивается произведение: 13*14*15*16*17?
(Ответ: произведение оканчивается цифрой 0)
Рекомендуем посмотреть:
 Школьная олимпиада по математике 4 класс
Школьная олимпиада по математике 4 класс
 Решение нестандартных задач по математике в начальной школе
Решение нестандартных задач по математике в начальной школе
 Решение нестандартных задач по математике в начальной школе. Движение гусеницы
Решение нестандартных задач по математике в начальной школе. Движение гусеницы
 Решение нестандартных задач в начальной школе. "Задачи на уравнивание"
Решение нестандартных задач в начальной школе. "Задачи на уравнивание"
Похожие статьи:
Олимпиадные задания по литературному чтению, 3 - 4 класс
Олимпиадные задания по математике, 4 класс
Олимпиадные задания по математике, 3 класс
Олимпиадные математические задачи с ответами, 3-4 класс
Олимпиадные задания с ответами по математике для 1-4 классов
Участник №2 профессионального конкурса для педагогов «Коллекция педагогического мастерства и творчества» с 15 августа по 15 ноября 2015 года
← Конспект урока по изобразительному искусству 2 класс. Сказочная птица | Модульное оригами Клубника. Мастер-класс с пошаговыми фото →
|
|
Автор: Елена Владимировна Петрюк
Опубликовано: 3555 дней назад (17 июля 2015)
Просмотров: 10866
Рубрика: Без рубрики
|
+5↑ Голосов: 5 |
| # 19 июля 2015 в 20:36 +1 |
| # 25 июля 2015 в 10:12 0 |
| # 16 сентября 2015 в 18:37 0 | ||
|
| # 20 сентября 2015 в 14:51 0 |
| # 29 октября 2015 в 17:56 0 |
| # 31 октября 2015 в 11:41 0 | ||
|
| # 10 ноября 2015 в 10:50 0 | ||
|


